��Ŀ����
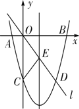
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪������y=ax2+bx-8��x�ύ��A��B���㣬��y�ύ�ڵ�C��ֱ��l��������ԭ��O���������ߵ�һ������ΪD���������ߵĶԳ��ύ�ڵ�E������CE����֪��A��D������ֱ�Ϊ��-2��0������6��-8����
��1���������ߵĺ�������ʽ�����ֱ������B�͵�E�����ꣻ
��2������P��y�Ḻ�����ϵ�һ�����㣬��������Ϊ��0��m����ֱ��PB��ֱ��l���ڵ�Q����̽������mΪ��ֵʱ����OPQ�ǵ��������Σ�
���𰸡�(1)y��![]() x2��3x��8��B(8��0),E(3����4)��(2)m��ֵΪ��
x2��3x��8��B(8��0),E(3����4)��(2)m��ֵΪ��![]() ��
��![]() .
.
��������
��1�����ݴ���ϵ������������߽���ʽ���������B���꣬���ֱ��OD����ʽ���ɽ����E������
��2������ͼ1�У���OP=OQʱ����OPQ�ǵ��������Σ�����E��ֱ��ME��PB����y���ڵ�M����x���ڵ�H�������M��H�����꼴�ɽ�����⣮����ͼ2�У���QO=QPʱ����POQ�ǵ��������Σ���֤��CE��PQ������ƽ���ߵ������г����̼��ɽ�����⣮
��1����������y��ax2��bx��8������A(��2��0)��D(6����8)��
�ཫA��D�������������![]() ��
��
���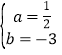 ��
��
�������ߵĺ�������ʽΪy��![]() x2��3x��8��
x2��3x��8��
��2�������������������ۣ�
�ٵ�OP��OQʱ����OPQ�ǵ��������Σ����ͼ����
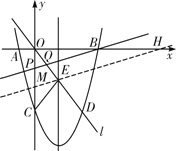
ͼ1
�ߵ�E������Ϊ(3����4)��
��OE��![]() ��5��
��5��
����E��ֱ��ME��PB����y���ڵ�M����x���ڵ�H��
��![]() ��
��![]() ��
��
��OM��OE��5��
���M������Ϊ(0����5)��
��ֱ��ME�ĺ�������ʽΪy��k1x��5��E��3��-4����ֱ��ME�ϣ�
��3k1��5����4�����k1��![]() ��
��
��ֱ��ME�ĺ�������ʽΪy��![]() x��5��
x��5��
��y��0�����x��15��
���H������Ϊ(15��0)��
�֡�MH��PB��
��![]() ��
��![]() ����
����![]() ��
��
��m����![]() ��
��
�ڵ�QO��QPʱ����OPQ�ǵ��������Σ���ͼ��
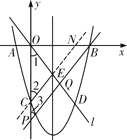
�ߵ�x��0ʱ��y��![]() x2��3x��8����8��
x2��3x��8����8��
���C������Ϊ(0����8)��
��CE��![]() ��5��
��5��
��OE��CE��
���1����2��
�֡�QO��QP��
���1����3��
���2����3��
��CE��PB.
��ֱ��CE��x���ڵ�N���亯������ʽΪy��k2x��8��
E��3��-4����ֱ��CE�ϣ�
��3k2��8����4�����k2��![]() ��
��
��ֱ��CE�ĺ�������ʽΪy��![]() x��8��
x��8��
��y��0����![]() x��8��0��
x��8��0��
��x��6��
���N������Ϊ(6��0)��
��CN��PB.
��![]() ��
��![]() ��
��
��![]() ��
��![]() �����m����
�����m����![]() .
.
������������m��ֵΪ��![]() ��
��![]() ʱ����OPQ�ǵ��������Σ�
ʱ����OPQ�ǵ��������Σ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�