题目内容
 如图所示是抛物线y=ax2+bx+c,刘星同学观察图象后,得出下列4个结论:①b2-4ac>0;②c>1;③2a-b<0;④a+b+c<0.你认为错误的有
如图所示是抛物线y=ax2+bx+c,刘星同学观察图象后,得出下列4个结论:①b2-4ac>0;②c>1;③2a-b<0;④a+b+c<0.你认为错误的有1
1
个.分析:①根据二次函数图象与x轴有两个交点,判别式△>0解答;
②根据二次函数图象与y轴的交点结合图形解答;
③根据二次函数图象对称轴x>-1,开口向下,a<0,整理即可得解;
④根据x=1时的y值的情况解答.
②根据二次函数图象与y轴的交点结合图形解答;
③根据二次函数图象对称轴x>-1,开口向下,a<0,整理即可得解;
④根据x=1时的y值的情况解答.
解答:解:①∵函数与x轴有两个交点,
∴方程ax2+bx+c=0有两个不相等的实数根,
∴b2-4ac>0,故本小题正确;
②结合图形,二次函数图象与y轴的正半轴相交,
故当x=0时可知,c=1,故本小题错误;
③∵二次函数图象开口向下,
∴a<0,
又∵-
>-1,
∴b>2a,
整理得,2a-b<0,故本小题正确;
④由图可知,当x=1时,y<0,
即a+b+c<0,故本小题正确.
综上所述,错误的有②共1个.
故答案为:1.
∴方程ax2+bx+c=0有两个不相等的实数根,
∴b2-4ac>0,故本小题正确;
②结合图形,二次函数图象与y轴的正半轴相交,
故当x=0时可知,c=1,故本小题错误;
③∵二次函数图象开口向下,
∴a<0,
又∵-
| b |
| 2a |
∴b>2a,
整理得,2a-b<0,故本小题正确;
④由图可知,当x=1时,y<0,
即a+b+c<0,故本小题正确.
综上所述,错误的有②共1个.
故答案为:1.
点评:本题考查了二次函数图象与系数的关系,熟练掌握二次函数的性质,开口方向、对称轴解析式、与y轴的交点坐标与系数的关系,并利用特殊自变量所对应的函数值的正负情况是解题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
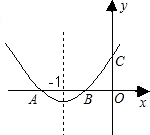 已知:如图所示,抛物线y=ax2+bx+c的对称轴为x=-1,与x轴交于A、B两点,交y轴于点C,且OB=OC,则下列结论正确的个数是( )
已知:如图所示,抛物线y=ax2+bx+c的对称轴为x=-1,与x轴交于A、B两点,交y轴于点C,且OB=OC,则下列结论正确的个数是( ) 如图所示是抛物线y=ax2+bx+c,刘星同学观察图象后,得出下列4个结论:①b2-4ac>0;②c>1;③2a-b<0;④a+b+c<0.你认为错误的有________个.
如图所示是抛物线y=ax2+bx+c,刘星同学观察图象后,得出下列4个结论:①b2-4ac>0;②c>1;③2a-b<0;④a+b+c<0.你认为错误的有________个.
