Question

一座拱型桥，桥下的水面宽度AB是20米，拱高CD是4米．若水面上升3米至EF，则水面宽度EF为多少？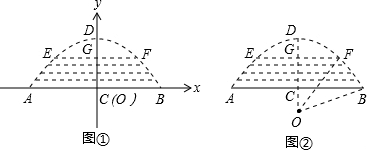

（1）若把它看作抛物线的一部分，在坐标系中（如图①），可设抛物线的表达式为y=ax²+c．请你填空：a=

 

，c=

 

，EF=

 

米；
（2）若把它看作圆的一部分，可构造图形（如图②）请你计算：
（3）请你估计（2）中EF与（1）中的EF的差的近似值（误差小于0.1米）．

Answer 1

分析：（1）可设：解析式为y=ax²+c令x=0，y=4，所以c=4；令x=10，100a+4=0，a=-0.04=-

1

25

，即解析式为y=-

1

25

x²+4，令y=3，x=±5，所以EF=10米；
（2）在Rt△BOC中先求出半径的长，再在Rt△FOG中，根据勾股定理求得FG的长，即可得EF得长；
（3）求差即可，注意保留到0.1即可．

解答：解：（1）设解析式为y=ax²+c
令x=0，y=4，
所以c=4；令x=10，100a+4=0，a=-0.04=-

1

25

∴解析式为y=-

1

25

x²+4
令y=3，x=±5，
所以EF=10米
∴a=-

1

25

，c=4，EF=10；（每格1分）

（2）设半径为x，在Rt△BOC中，OC=x-4
∴（x-4）²+10²=x²
∴x=

29

2

在Rt△FOG中，FG=

( 29 2 )2-( 29 2 -1)2

=2

7

∴EF=4

7

；（3分）

（3）4

7

-10≈4×2.646-10≈0.6（2分）．

点评：此题考查了现实中的二次函数问题以及垂径定理和勾股定理的实际应用．