题目内容
如图,在⊙O中,AB、AC是互相垂直且相等的两条弦,OD⊥AB,OE⊥AC,垂足分别为D、E,若AC=2cm,则⊙O的半径为 cm.
【答案】分析:易证ADOE为正方形,且边长为1,对角线AO的长即为半径.
解答: 解:∵OD⊥AB,
解:∵OD⊥AB,
∴AD=BD= AB.
AB.
同理AE=CE= AC.
AC.
∵AB=AC,∴AD=AE.
连接OA,∵OD⊥AB OE⊥AC AB⊥AC,
∴∠OEA=∠A=∠ODA=90°,
∴ADOE为矩形.
又∵AD=AE,∴ADOE为正方形,
∴OA= =
= (cm).
(cm).
点评:解此类题一般要把半径、弦心距、弦的一半构建在一个直角三角形里,运用勾股定理求解.
解答:
 解:∵OD⊥AB,
解:∵OD⊥AB,∴AD=BD=
 AB.
AB.同理AE=CE=
 AC.
AC.∵AB=AC,∴AD=AE.
连接OA,∵OD⊥AB OE⊥AC AB⊥AC,
∴∠OEA=∠A=∠ODA=90°,
∴ADOE为矩形.
又∵AD=AE,∴ADOE为正方形,
∴OA=
 =
= (cm).
(cm).点评:解此类题一般要把半径、弦心距、弦的一半构建在一个直角三角形里,运用勾股定理求解.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
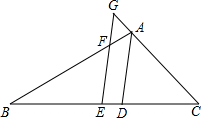 如图,在△ABC中,AB>AC,E为BC边的中点,AD为∠BAC的平分线,过E作AD的平行线,交AB于F,交CA的延长线于G.
如图,在△ABC中,AB>AC,E为BC边的中点,AD为∠BAC的平分线,过E作AD的平行线,交AB于F,交CA的延长线于G.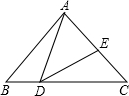 如图,在△ABC中,AB=AC,D为BC边上一点,且∠BAD=30°,若AD=DE,∠EDC=33°,则∠DAE的度数为
如图,在△ABC中,AB=AC,D为BC边上一点,且∠BAD=30°,若AD=DE,∠EDC=33°,则∠DAE的度数为 如图,在△ABC中,AB=AC,D是△ABC内一点,且BD=DC.求证:∠ABD=∠ACD.
如图,在△ABC中,AB=AC,D是△ABC内一点,且BD=DC.求证:∠ABD=∠ACD.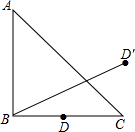 如图,在△ABC中,AB=BC,∠ABC=90°,D是BC的中点,且它关于AC的对称点是D′,BD′=
如图,在△ABC中,AB=BC,∠ABC=90°,D是BC的中点,且它关于AC的对称点是D′,BD′=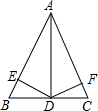 如图,在△ABC中,AB=AC,D点是BC的中点,DE⊥AB于E点,DF⊥AC于F点,则图中全等三角形共有
如图,在△ABC中,AB=AC,D点是BC的中点,DE⊥AB于E点,DF⊥AC于F点,则图中全等三角形共有