Question

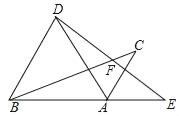
【题目】如图，已知直线AB，CD被直线AC所截，AB∥CD，E是平面内任意一点（点E不在直线AB，CD，AC上），设∠BAE=α，∠DCE=β．下列各式：①α+β，②α﹣β，③180°﹣α﹣β，④360°﹣α﹣β，∠AEC的度数可能是（ ）

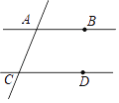
A. ①②③ B. ①②④C. ①③④ D. ①②③④

Answer 1

【答案】B

【解析】

根据E点有4中情况，分四种情况讨论分别画出图形，根据平行线的性质与三角形外角定理求解.

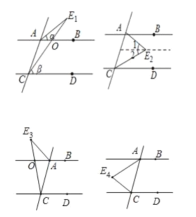
E点有4中情况，分四种情况讨论如下：

由AB∥CD，可得∠AOC=∠DCE1=β

∵∠AE1C=∠BAE1+∠AE1C，

∴∠AE1C=β-α

过点E2作AB的平行线，由AB∥CD，

可得∠1=∠BAE2=α,∠2=∠DCE2=β

∴∠AE2C=α+β

由AB∥CD，可得∠BOE3=∠DCE3=β

∵∠BAE3=∠BOE3+∠AE3C，

∴∠AE3C=α-β

由AB∥CD，可得

∠BAE4+∠AE4C+∠DCE4=360°，

∴∠AE4C=360°-α-β

∴∠AEC的度数可能是①α+β，②α﹣β，④360°﹣α﹣β，故选B.