题目内容
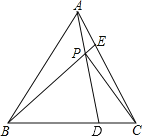
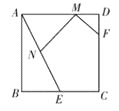
【题目】在等腰直角三角形![]() 中,
中,![]() ,
,![]() .点
.点![]() 为射线
为射线![]() 上一个动点,连接
上一个动点,连接![]() ,点
,点![]() 在直线
在直线![]() 上,且
上,且![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,点
,点![]() ,
,![]() 在直线
在直线![]() 的同侧,且
的同侧,且![]() ,连接
,连接![]() .请用等式表示线段
.请用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系.小明根据学习函数的经验.对线段
之间的数量关系.小明根据学习函数的经验.对线段![]() ,
,![]() ,
,![]() 的长度之间的关系进行了探究.下面是小明的探究过程,请补充完整:
的长度之间的关系进行了探究.下面是小明的探究过程,请补充完整:
(1)对于点![]() 在射线
在射线![]() 上的不同位置,画图、测量,得到了线段
上的不同位置,画图、测量,得到了线段![]() ,
,![]() ,
,![]() 的长度的几组值,如下表:
的长度的几组值,如下表:
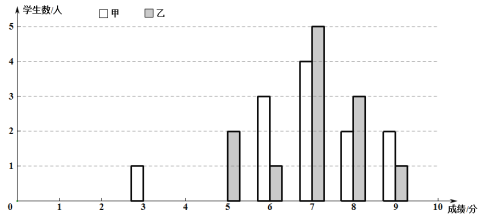
位置 1 | 位置 2 | 位置 3 | 位置 4 | 位置 5 | 位置 6 | 位置 7 | 位置 8 | |
| 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 |
| 2.10 | 1.32 | 0.53 | 0.00 | 1.32 | 2.10 | 4.37 | 5.6 |
| 0.52 | 1.07 | 1.63 | 2.00 | 2.92 | 3.48 | 5.09 | 5.97 |
在![]() ,
,![]() ,
,![]() 的长度这三个量中,确定 的长度是自变量, 的长度是这个自变量的函数, 的长度是常量.
的长度这三个量中,确定 的长度是自变量, 的长度是这个自变量的函数, 的长度是常量.
(2)在同一平面直角坐标系![]() 中,画出(1)中所确定的函数的图象;
中,画出(1)中所确定的函数的图象;
(3)结合函数图象,解决问题:请用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系.
之间的数量关系.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]()
【解析】
(1)按照变量的定义,根据题意点P为动点,BE的长随着点P的移动而改变,BC为已知等腰直角三角形![]() 的斜边;
的斜边;
(2)描点画出图象即可;
(3)根据图形可求出![]() 长度根据
长度根据![]() 长度变化的函数关系式为一次函数,发现斜率绝对值接近
长度变化的函数关系式为一次函数,发现斜率绝对值接近![]() ,再通过画图可证明三条线段关系.
,再通过画图可证明三条线段关系.
(1)根据题意,画出图形,再结合表格数据可知,![]() 的长度是自变量,
的长度是自变量,![]() 的长度是这个自变量的函数,
的长度是这个自变量的函数,![]() 的长度是常量.
的长度是常量.
故答案为:![]() ,
,![]() ,
,![]() .
.
(2)根据表格数据描点画出以下图像
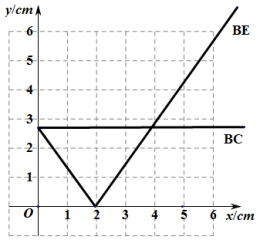
(3)首先通过函数图像图像,可判断BE关于BP的函数图像氛围两部分,斜率接近![]() ,则可知线段
,则可知线段![]() ,
,![]() ,
,![]() 之间的数量关系
之间的数量关系![]() .
.
再通过画图证明:
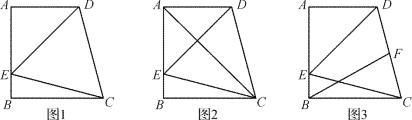
当点P在线段BA的延长线上时,如图,过点P作PF垂直于AC交BC的延长线于F,
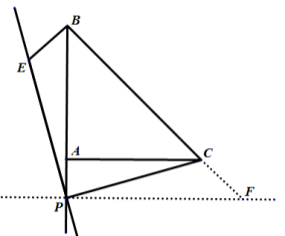
∵![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() (
(![]() ),
),
∴![]() ,
,
在等腰直角三角形![]() 中,
中,![]()
∴![]() ,
,
即,![]() ;
;
当点P在线段AB上时,过点P作![]() 于点
于点![]() ,
,
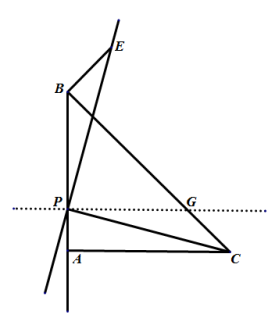
同理可证![]() (
(![]() ),
),
∴![]() ,
,
∴![]() ,
,
又∵![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
∴![]()
综上:线段![]() ,
,![]() ,
,![]() 之间的数量关系为:
之间的数量关系为:![]() .
.