��Ŀ����
��ͼ1��������y=x2�Ķ���ΪP��A��B�������������㣬AB��x�ᣬ�ı���ABCDΪ���Σ�CD�߾�����P��AB=2AD����1�������ABCD�������
��2����ͼ2�����������ߡ�y=x2������Ϊ�����ߡ�y=x2+bx+c���������������䣬��������ABCD�������
��3�����������ߡ�y=x2+bx+c����Ϊ�����ߡ�y=ax2+bx+c���������������䣬��������ABCD�����������a��b��c��ʾ����ֱ��д���𰸣�
�����⣺�������С�y=x2����Ϊ��y=ax2+bx+c������AB=2AD��������Ҫ�������������䣬̽������ABCD��
 ��Ϊ����ʱ������ABCD��Ҫ����ʲô������˵�����ɣ�
��Ϊ����ʱ������ABCD��Ҫ����ʲô������˵�����ɣ�
��������1����AD=m���ó�AB=2m����Ϊ����������Գ�ͼ�Σ������A�����꣮Ȼ���������ABCD�������
��2����������y=x2+bx+c����AD=m��AB=2m�������A������Ϊ��h-m��n+m����Ȼ����������ABCD�������
��3����������y=ax2+bx+c����AD=m��
=k�ó�AB=km���������ABCD����ı���ʽ�������ۣ�
��2����������y=x2+bx+c����AD=m��AB=2m�������A������Ϊ��h-m��n+m����Ȼ����������ABCD�������
��3����������y=ax2+bx+c����AD=m��
| AB |
| AD |
����⣺��1����AD=m��
��AB=2AD��
��AB=2m��������������Գ�ͼ�Σ�
��PD=m��
���A��������-m��m����
��m2=m��
�֡�m��0��
��m=1
�����ABCD�����Ϊ1��2=2��
��2����������y=x2+bx+c=��x-h��2+n��
���P��������h��n����
��AD=m��
��AB=2AD��
��AB=2m��
�֡�����������Գ�ͼ�Σ�
��PD=m��
���A��������h-m��n+m����
��n+m=��h-m-h��2+n��
��m=m2��
�֡�m��0��
��m=1��
�����ABCD�����Ϊ1��2=2��
��3��
�����⣺
�⣺
������
��������y=ax2+bx+c=a��x-h��2+n��
���P��������h��n����
��AD=m��
=k��
��AB=km��
�֡�����������Գ�ͼ�Σ�
��PD=
���A��������h-
��n+m����
��n+m=a��h-
-h��2+n��
��m=
��
�֡�m��0��
��m=
��
�����ABCD�����Ϊkm2=
��a������
��kΪ����ʱ������ABCD�����Ϊ������
��
Ϊ����ʱ������ABCD�����Ϊ������
��AB=2AD��
��AB=2m��������������Գ�ͼ�Σ�
��PD=m��
���A��������-m��m����
��m2=m��
�֡�m��0��
��m=1
�����ABCD�����Ϊ1��2=2��
��2����������y=x2+bx+c=��x-h��2+n��
���P��������h��n����
��AD=m��
��AB=2AD��
��AB=2m��
�֡�����������Գ�ͼ�Σ�
��PD=m��
���A��������h-m��n+m����
��n+m=��h-m-h��2+n��
��m=m2��
�֡�m��0��
��m=1��
�����ABCD�����Ϊ1��2=2��
��3��
| 2 |
| a2 |
�����⣺
�⣺
| AB |
| AD |
��������y=ax2+bx+c=a��x-h��2+n��
���P��������h��n����
��AD=m��
| AB |
| AD |
��AB=km��
�֡�����������Գ�ͼ�Σ�
��PD=
| km |
| 2 |
���A��������h-
| km |
| 2 |
��n+m=a��h-
| km |
| 2 |
��m=
| ak2m2 |
| 4 |
�֡�m��0��
��m=
| 4 |
| ak2 |
�����ABCD�����Ϊkm2=
| 16 |
| a2k3 |
��a������
��kΪ����ʱ������ABCD�����Ϊ������
��
| AB |
| AD |
�����������ۺϿ����˶��κ��������֪ʶ�Լ�����ABCD����ļ��㹫ʽ���ѶȽϴ�

��ϰ��ϵ�д�
 ��ĩ��ϰ���ϵ�д�
��ĩ��ϰ���ϵ�д� ����ѧ�䵥Ԫ������ĩר����100��ϵ�д�
����ѧ�䵥Ԫ������ĩר����100��ϵ�д� �Ƹ�360�ȶ����ܾ�ϵ�д�
�Ƹ�360�ȶ����ܾ�ϵ�д� ���⿼����Ԫ���Ծ�ϵ�д�
���⿼����Ԫ���Ծ�ϵ�д�
�����Ŀ
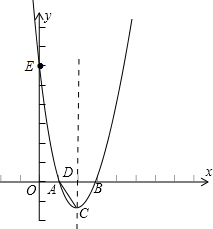 ��֪���κ�����ͼ���Ǿ�����A��1��0����B��3��0����E��0��6�������һ�������ߣ�
��֪���κ�����ͼ���Ǿ�����A��1��0����B��3��0����E��0��6�������һ�������ߣ� �Ķ����ϣ���ͼ1������ABC����������ֱ�������ˮƽ�ߴ�ֱ������ֱ�ߣ��������ֱ��֮��ľ���С�ABC�ġ�ˮƽ������a�����м������ֱ���ڡ�ABC�ڲ��߶εij��ȽС�ABC�ġ�Ǧ���ߡ���h�������ǿɵó�һ�ּ���������������·�����S��ABC=
�Ķ����ϣ���ͼ1������ABC����������ֱ�������ˮƽ�ߴ�ֱ������ֱ�ߣ��������ֱ��֮��ľ���С�ABC�ġ�ˮƽ������a�����м������ֱ���ڡ�ABC�ڲ��߶εij��ȽС�ABC�ġ�Ǧ���ߡ���h�������ǿɵó�һ�ּ���������������·�����S��ABC=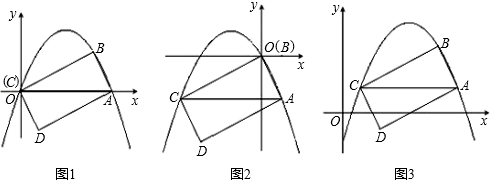
 ��ͼ����������
��ͼ����������