题目内容
在Rt△ABC中,斜边AB=4,∠B=60°.将△ABC绕点B按顺时针方向旋转60°,顶点C运动的路线长是
- A.

- B.

- C.π
- D.
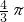
B
分析:利用三角函数求得BC的长,顶点C运动的路线是以B为圆心,以60°为圆心角,半径是BC的弧,利用弧长公式即可求解.
解答:∵在Rt△ABC中,斜边AB=8,∠B=60°,
∴BC=AB•cosB=4× =2,
=2,
∴顶点C运动的路线长是: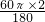 =
= .
.
故选B.
点评:本题考查了弧长的计算公式,正确求得半径BC的长度,理解弧长的计算公式是关键.
分析:利用三角函数求得BC的长,顶点C运动的路线是以B为圆心,以60°为圆心角,半径是BC的弧,利用弧长公式即可求解.
解答:∵在Rt△ABC中,斜边AB=8,∠B=60°,
∴BC=AB•cosB=4×
 =2,
=2,∴顶点C运动的路线长是:
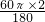 =
= .
.故选B.
点评:本题考查了弧长的计算公式,正确求得半径BC的长度,理解弧长的计算公式是关键.

练习册系列答案
相关题目
 的位置,其中
的位置,其中 分别是A、B对应点,且点B在斜边
分别是A、B对应点,且点B在斜边 交AB于D,这时∠BDC的度数是
交AB于D,这时∠BDC的度数是

 的位置,其中
的位置,其中 分别是A、B对应点,且点B在斜边
分别是A、B对应点,且点B在斜边 交AB于D,这时∠BDC的度数是
交AB于D,这时∠BDC的度数是