题目内容
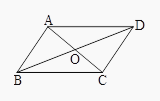
【题目】已知如图所示， 
与 
关于点 
成中心对称，连接 
， 
．
（1）求证：四边形 
是平行四边形；
（2）若 的面积为15 
，求四边形 的面积．
【答案】
（1）
证明：∵ 
与 
关于点 
成中心对称，∴ 
即四边形 
的对角线互相平分，∴四边形 
是平行四边形.
（2）
解：记 底边上的高为h，那么平行四边形ABCD底边AB上的为2h，因为 的面积为15，所以 
，所以2ABh＝60，所以平行四边形ABCD的面积为60 
．
【解析】（2）的关键在于明白： 底边上的高为平行四边形ABCD底边AB上的为一半．
【考点精析】根据题目的已知条件，利用平行四边形的判定和中心对称及中心对称图形的相关知识可以得到问题的答案，需要掌握两组对边分别平行的四边形是平行四边形：两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；两组对角分别相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形；如果把一个图形绕着某一点旋转180度后能与另一个图形重合，那么我们就说，这两个图形成中心对称；如果把一个图形绕着某一点旋转180度后能与自身重合，那么我们就说，这个图形成中心对称图形．
练习册系列答案
相关题目
