题目内容
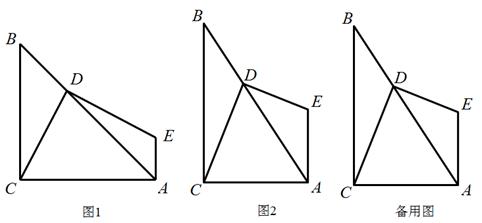
如图,在□ABCD中,E是AB的中点,ED和AC相交于点F,过点F作FG∥AB,交AD于点G.
(1)求证:AB=3FG;
(2)若AB:AC=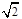 :
: ,求证:
,求证: .
.
见解析.
解析试题分析:(1)平行四边形的性质、线段中点的定义推知AF:FC=EF:ED=1:2.然后由平行线的性质和平行线分线段成比例得得到:FG:CD=AF:AC=1:3,所以FG:AB=1:3,即AB=3FG;
(2)根据已知条件可以设AB= k,AC=
k,AC= k,则AE=
k,则AE= k,AF=
k,AF= k.通过证△AEF∽△ACB,得到对应角∠AEF=∠ACB.然后易证△FDG∽△ADF,所以DF:DA=DG:DF,即DF2=DG•DA.
k.通过证△AEF∽△ACB,得到对应角∠AEF=∠ACB.然后易证△FDG∽△ADF,所以DF:DA=DG:DF,即DF2=DG•DA.
试题解析:
证明:(1)在□ABCD中,AB∥CD,AB=CD,AD∥BC,
又∵E是AB的中点,∴ ,
,
∵FG∥AB,∴FG∥CD,∴ ,
,
∴ ,∴AB=3FG.
,∴AB=3FG.
(2)设AB= k,AC=
k,AC= k,
k,
则AE= k,AF=
k,AF= k.
k.
∴ ,
, ,
,
∴ .
.
又∵∠EAF=∠CAB,∴△AEF∽△ACB,∴∠AEF=∠ACB.
∵FG∥AB,AD∥BC;∴∠AEF=∠DFG,∠ACB=∠DAF,
∴∠DFG=∠DAF.
又∵∠FDG=∠ADF,∴△FDG∽△ADF,
∴ ,∴
,∴ .
.
考点:1.相似三角形的判定与性质;2.平行四边形的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 的值。(2)线段GH的长。
的值。(2)线段GH的长。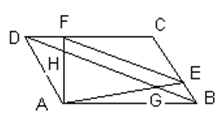
 是
是 上一点,
上一点, ∥
∥ ,
, 分别交
分别交 于点
于点 ,∠1=∠2,探索线段
,∠1=∠2,探索线段 之间的关系,并说明理由.
之间的关系,并说明理由.

 .
.
 ,在同一时刻测得小丽和建筑物
,在同一时刻测得小丽和建筑物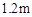 和
和 ,求建筑物
,求建筑物