题目内容
如图，在
中，
，
为
中点，四边形
是平行四边形．求证：四边形
是矩形．
中，，为中点，四边形是平行四边形．求证：四边形是矩形．证明见解析
证明：∵四边形是平行四边形，∴
∥，
，
．
∵为的中点，∴
．
∵
∥，
．∴四边形是平行四边形．…………………（7分）
∵，∴
，
∴平行四边形是矩形．（方法不唯一）……………………………………（8分）
已知四边形ABDE是平行四边形，只需证得它的一个内角是直角即可；在等腰△ABC中，AD是底边的中线，根据等腰三角形三线合一的性质即可证得∠ADC是直角，由此得证．
是平行四边形，∴∥，，．∵
为的中点，∴．∵
∥，．∴四边形是平行四边形．…………………（7分）∵
，∴，∴平行四边形
是矩形．（方法不唯一）……………………………………（8分）已知四边形ABDE是平行四边形，只需证得它的一个内角是直角即可；在等腰△ABC中，AD是底边的中线，根据等腰三角形三线合一的性质即可证得∠ADC是直角，由此得证．
练习册系列答案
相关题目
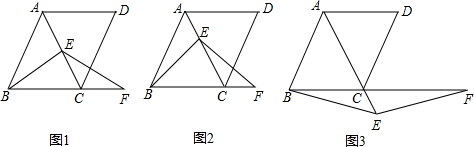
绕着点
，按顺时针方向旋转得到正方形
，边
与
交于点
（如图）．试问线段
与线段
相等吗？请先观察猜想，然后再证明你的猜想．
中，
∥
，
，
，
，则梯形
中，
，对角线BD=7，则菱形
，∠CAB=30°，AB= 6
。