Question

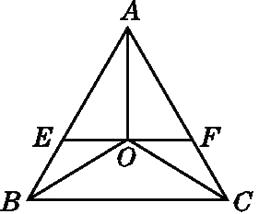
【题目】如图,在△ABC中,AB=AC,△ABC的角平分线BD和CE相交于O点,则图中的全等三角形共有( )

A.1对
B.2对
C.3对
D.4对

Answer 1

【答案】C
【解析】解：①△BCE≌△CBD理由：
∵AB=AC ,
∴∠B=∠C ,
∵△ABC的角平分线BD和CE相交于O点 ,
∴ ∠ABD=∠DBC=∠ABC ,∠ACE=∠ECB=∠ACB ,
∴∠DBC=∠ECB ,
∵ BC=CB ,
∴△BCE≌△CBD；
②△BOE≌△COD理由：
∵∠ABD=∠DBC=∠ABC ,∠ACE=∠ECB=∠ACB ,∠B=∠C ,
∴∠EBO=∠DCO ,
∵△BCE≌△CBD ,
∴BE=CD ,
又∵∠EOB=∠DOC，
∴△BOE≌△COD；
③△ABD≌△ACE理由：
∵AB=AC，∠A=∠A，∠ABD=∠ACE ，
∴△ABD≌△ACE．
故应选：C 。
根据等边对等角得出∠B=∠C ,根据角平分线的定义及等量代换得出∠DBC=∠ECB ,又BC=CB ，从而利用ASA判断出△BCE≌△CBD ；根据角平分线的定义得出∠EBO=∠DCO ,根据全等三角形对应边相等得出BE=CD ,又∠EOB=∠DOC，从而利用AAS判断出△BOE≌△COD；利用ASA就能判断出△ABD≌△ACE，从而得出结论。