题目内容
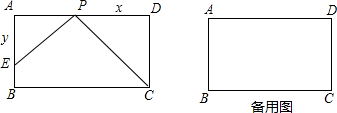
已知矩形ABCD中,AD=nAB,E为AB的中点,BF⊥CE于点F,过点F作DF的垂线交直线BC于G.
(1)如图1,当n=1时,求证:△BFG∽△CFD;
(2)如图2,当n=2时,求证:CG=7BG.

(1)证明:∵四边形ABCD是矩形,AB=AD,
∴四边形ABCD是正方形,
∴AB∥CD,∠ABC=90°,
∴∠BEC+∠BCE=90°,
∵BF⊥CE,
∴∠FBC+∠BCE=90°,
∴∠FBC=∠BEC,
∵AB∥CD,
∴∠BEC=∠DCE,
∴∠FBC=∠DCF,
∵BF⊥EC,FG⊥DF,
∴∠BFC=∠DFG=90°,
∴∠BFG=∠DFC=90°-∠GFC,
∵∠FBC=∠DCF,
∴△BFG∽△CFD.
(2)证明:∵四边形ABCD是矩形,
∴∠ABC=90°,AD=BC,AB=CD,
∵AD=2AB,AB=2BE,
∴AD=BC=4BE,
即 =
= ,
,
∵∠CBE=∠BFC=90°,∠FCB=∠FCB,
∴△CFB∽△CBE,
∴ =
= =
= ,
,
∵△BFG∽△CFD,
∴ =
= =
= ,
,
即CD=4BG,
∵AD=BC=2AB=2CD,
∴BC=8BG,
∴CG=BC-BG=7BG.
分析:(1)根据矩形性质得出AB∥CD,∠ABC=90°,求出∠FBC=∠BEC=∠DCF,根据相似三角形的判定推出即可.
(2)求出AD=BC=4BE,推出 =
= ,证△CFB∽△CBE,求出
,证△CFB∽△CBE,求出 =
= =
= ,求出
,求出 =
= =
= ,推出CD=4BG,求出BC=8BG即可.
,推出CD=4BG,求出BC=8BG即可.
点评:本题考查了平行线的性质,矩形的性质,相似三角形的性质和判定的应用,主要考查学生运用定理进行推理的能力.
∴四边形ABCD是正方形,
∴AB∥CD,∠ABC=90°,
∴∠BEC+∠BCE=90°,
∵BF⊥CE,
∴∠FBC+∠BCE=90°,
∴∠FBC=∠BEC,
∵AB∥CD,
∴∠BEC=∠DCE,
∴∠FBC=∠DCF,
∵BF⊥EC,FG⊥DF,
∴∠BFC=∠DFG=90°,
∴∠BFG=∠DFC=90°-∠GFC,
∵∠FBC=∠DCF,
∴△BFG∽△CFD.
(2)证明:∵四边形ABCD是矩形,
∴∠ABC=90°,AD=BC,AB=CD,
∵AD=2AB,AB=2BE,
∴AD=BC=4BE,
即
 =
= ,
,∵∠CBE=∠BFC=90°,∠FCB=∠FCB,
∴△CFB∽△CBE,
∴
 =
= =
= ,
,∵△BFG∽△CFD,
∴
 =
= =
= ,
,即CD=4BG,
∵AD=BC=2AB=2CD,
∴BC=8BG,
∴CG=BC-BG=7BG.
分析:(1)根据矩形性质得出AB∥CD,∠ABC=90°,求出∠FBC=∠BEC=∠DCF,根据相似三角形的判定推出即可.
(2)求出AD=BC=4BE,推出
 =
= ,证△CFB∽△CBE,求出
,证△CFB∽△CBE,求出 =
= =
= ,求出
,求出 =
= =
= ,推出CD=4BG,求出BC=8BG即可.
,推出CD=4BG,求出BC=8BG即可.点评:本题考查了平行线的性质,矩形的性质,相似三角形的性质和判定的应用,主要考查学生运用定理进行推理的能力.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 ,点Q从点B以每秒1个单位沿BA方向向点A运动,设运动时间为t秒,△BPQ的面积为S.
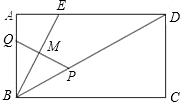
,点Q从点B以每秒1个单位沿BA方向向点A运动,设运动时间为t秒,△BPQ的面积为S. 如图,已知矩形ABCD中,BC=6,AB=8,延长AD到点E,使AE=15,连接BE交AC于点P.
如图,已知矩形ABCD中,BC=6,AB=8,延长AD到点E,使AE=15,连接BE交AC于点P. 如图:已知矩形ABCD中,CE∥DF.
如图:已知矩形ABCD中,CE∥DF.