题目内容
【题目】已知，如图，抛物线y = ax2 + bx + c
交x轴于A(4，0)，C(-1，0)两点，交y轴于点B(0，3) ．
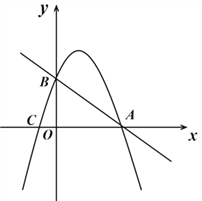
（1）求抛物线y = ax2 + bx + c的解析式；
（2）点P是抛物线（在点A与点B之间的部分）上的点，求△ABP的面积最大值；
（3）若点M在y轴上，且△ABM为等腰三角形，请直接写出M点坐标．
【答案】(1) 
; (2)6;(3) M坐标为(0，8)或 (0，-2) 或(0，-3) 或(0，
).
【解析】分析：
用待定系数法确定函数关系式即可.
用待定系数法求出直线
的解析式，设点P的横坐标为m，作PD⊥x轴交AB于点D，表示出△ABP的面积，根据二次函数的性质即可求出最大值.
分三种情况进行讨论:
详解：（1）将A(4，0)、 B(0，3)、C(-1，0)代入得
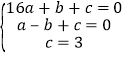，解得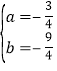
，∴
.
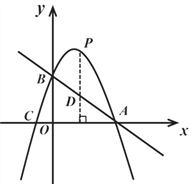
（2）设直线AB为y1=k1x+b，将A(4,0), B(0,3)代入得
，解得
，∴
.
设点P的横坐标为m，作PD⊥x轴交AB于点D,
∴
，
∴S△PBA=
OAPD=×4×(
)=
,
∴S△PBA的最大值 = 6,
（3）点M坐标为(0，8)或 (0，-2) 或(0，-3) 或(0，
).
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
期末集结号系列答案
相关题目
