题目内容
 如图,某商标是由边长均为2的正三角形、正方形、正六边形的金属薄片镶嵌而成的镶嵌图案.如果在这个镶嵌图案中随机确定一个点O,那么点O落在镶嵌图案中的正方形区域的概率为________.
如图,某商标是由边长均为2的正三角形、正方形、正六边形的金属薄片镶嵌而成的镶嵌图案.如果在这个镶嵌图案中随机确定一个点O,那么点O落在镶嵌图案中的正方形区域的概率为________.
( .结果保留二位小数)
.结果保留二位小数)
0.54
分析:由图形得到由10个正三角形,11个正方形,2个正六边形,分别求出三个图形的面积,即可求出点O落在镶嵌图案中的正方形区域的概率.
解答: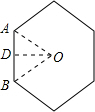 解:由图形可知:由10个正三角形,11个正方形,2个正六边形,正方形的面积是2×2=4,
解:由图形可知:由10个正三角形,11个正方形,2个正六边形,正方形的面积是2×2=4,
连接OA、OB,
∵图形是正六边形,
∴△OAB是等边三角形,且边长是2,
即等边三角形的面积是 ,
,
∴正六边形的面积是6× =6
=6 ,
,
∴点O落在镶嵌图案中的正方形区域的概率是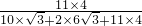 ≈0.54,
≈0.54,
答:点O落在镶嵌图案中的正方形区域的概率约为0.54.
故答案为:0.54.
点评:本题主要考查了正多边形与圆,等边三角形的性质和判定,几何概率,勾股定理,平面镶嵌等知识点的理解和掌握,能根据性质进行计算是解此题的关键.
分析:由图形得到由10个正三角形,11个正方形,2个正六边形,分别求出三个图形的面积,即可求出点O落在镶嵌图案中的正方形区域的概率.
解答:
 解:由图形可知:由10个正三角形,11个正方形,2个正六边形,正方形的面积是2×2=4,
解:由图形可知:由10个正三角形,11个正方形,2个正六边形,正方形的面积是2×2=4,连接OA、OB,
∵图形是正六边形,
∴△OAB是等边三角形,且边长是2,
即等边三角形的面积是
 ,
,∴正六边形的面积是6×
 =6
=6 ,
,∴点O落在镶嵌图案中的正方形区域的概率是
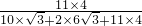 ≈0.54,
≈0.54,答:点O落在镶嵌图案中的正方形区域的概率约为0.54.
故答案为:0.54.
点评:本题主要考查了正多边形与圆,等边三角形的性质和判定,几何概率,勾股定理,平面镶嵌等知识点的理解和掌握,能根据性质进行计算是解此题的关键.

练习册系列答案
相关题目
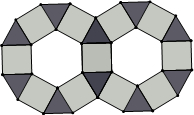 镶嵌图案.
镶嵌图案. (2012•锦江区一模)如图,某商标是由边长均为2的正三角形、正方形、正六边形的金属薄片镶嵌而成的镶嵌图案.如果在这个镶嵌图案中随机确定一个点O,那么点O落在镶嵌图案中的正方形区域的概率为
(2012•锦江区一模)如图,某商标是由边长均为2的正三角形、正方形、正六边形的金属薄片镶嵌而成的镶嵌图案.如果在这个镶嵌图案中随机确定一个点O,那么点O落在镶嵌图案中的正方形区域的概率为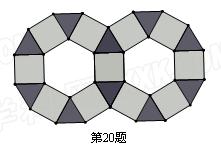
 是由边长均为2的正三角形、正方形、正六边形的金属薄片镶嵌而成的镶嵌图案.
是由边长均为2的正三角形、正方形、正六边形的金属薄片镶嵌而成的镶嵌图案.