题目内容
【题目】已知: 两直线![]() ,
,![]() ,且
,且![]() ∥CD,点
∥CD,点![]() ,
,![]() 分别在直线
分别在直线![]() ,
,![]() 上. 放置一个足够大的三角尺,使得三角尺的两边
上. 放置一个足够大的三角尺,使得三角尺的两边![]() ,
,![]() 分别经过点
分别经过点![]() ,
,![]() . 过点
. 过点![]() 作射线
作射线![]() ,使得
,使得![]() .
.
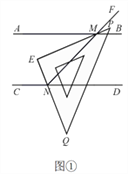
(1)转动三角尺,如图①所示,当射线![]() 与
与![]() 重合,
重合,![]() 时,则
时,则![]() ________;
________;
(2)转动三角尺,如图②所示,当射线![]() 与
与![]() 不重合,
不重合,![]() 时,求
时,求![]() 的度数.
的度数.
(3)转动直角三角尺的过程中, 请直接写出![]() 与
与![]() 之间的数量关系.
之间的数量关系.


【答案】(1)22.5°;(2)30°;(3)∠FND=2∠AME.
【解析】试题分析:(1)先根据平行线的性质和邻补角的性质求得∠AMN=![]() ,∠MNC=135 o,再由
,∠MNC=135 o,再由![]() 求得
求得![]() =67.5 o,再在直角三角形求得∠EMN=22.5 o,由∠AME=∠AMN-∠NME即可示得;
=67.5 o,再在直角三角形求得∠EMN=22.5 o,由∠AME=∠AMN-∠NME即可示得;
(2) 先根据平行线的性质和邻补角的性质求得∠AGN=![]() ,∠GNC=120 o,再由
,∠GNC=120 o,再由![]() 求得
求得![]() =60 o,再在直角三角形求得∠EHN=30 o,则∠GHM=30 o,由∠AME=∠AMN-∠NME即可示得;
=60 o,再在直角三角形求得∠EHN=30 o,则∠GHM=30 o,由∠AME=∠AMN-∠NME即可示得;
(3)由(1)(2)直接得出结论.
试题解析:
(1)∵AB//CD,
∴∠AMN=∠FND,
又∵![]() ,∠CNF+FND=180o,
,∠CNF+FND=180o,
∴∠AMN=![]() ,∠MNC=135 o,
,∠MNC=135 o,
又∵![]() ,
,
∴![]() =67.5 o,
=67.5 o,
又∵∠MEN=90 o,
∴∠EMN=90-67.5=22.5 o,
又∵∠NME+∠AME=∠AMN=45 o,
∴![]() 45 o-22.5 o=45 o;
45 o-22.5 o=45 o;
(2)如图所示:FN与AB相交于点G,FN相EM相交于点H,
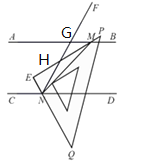
∵AB//CD,
∴∠AGN=∠FND,
又∵![]() ,∠CNG+GND=180o,
,∠CNG+GND=180o,
∴∠AGN=![]() ,∠GNC=120 o,
,∠GNC=120 o,
又∵![]() ,
,
∴![]() =60 o,
=60 o,
又∵∠MEN=90 o,
∴∠EHN=90-60=30 o,
∴∠GHM=30 o,
又∵∠AGH=∠GHM+∠GMH=60 o,
∴![]() 60 o-30 o=30 o;
60 o-30 o=30 o;
(3) ∠FND=2∠AME.

【题目】已知下表:
x | 0 | 1 | 2 |
ax2 | 1 | ||
ax2+bx+c | 3 | 3 |
(1)求a、b、c的值,并在表内空格处填入正确的数;
(2)请你根据上面的结果判断:
①是否存在实数x,使二次三项式ax2+bx+c的值为0?若存在,求出这个实数值;若不存在,请说明理由.
②画出函数y=ax2+bx+c的图象示意图,由图象确定,当x取什么实数时,ax2+ bx+c>0?