题目内容
已知函数y=ax2+bx+c的图象与函数y=
的图象的形状、开口方向都相同，且顶点坐标是（-2，4），求a、b、c的值．
解：∵函数y=ax2+bx+c的图象与函数y=的图象的形状、开口方向都相同，且顶点坐标是（-2，4），
∴抛物线的解析式为y=
（x+2）2+4=x2+2x+6，
∴a=，b=2，c=6．
分析：由于已知顶点坐标，则可表示出抛物线的解析式为y=（x+2）2+4，然后展开即可得到a、b、c的值．
点评：本题考查了二次函数与几何变换：由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．
的图象的形状、开口方向都相同，且顶点坐标是（-2，4），∴抛物线的解析式为y=
（x+2）2+4=x2+2x+6，∴a=
，b=2，c=6．分析：由于已知顶点坐标，则可表示出抛物线的解析式为y=
（x+2）2+4，然后展开即可得到a、b、c的值．点评：本题考查了二次函数与几何变换：由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．
练习册系列答案
相关题目
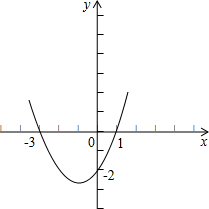已知函数y=ax2+bx+c的图象如图所示，试根据图象回答下列问题：