题目内容
已知AB是⊙O直径,AC是⊙O的弦,AB=2,∠BAC=30°,弦AD=1,那么∠CAD的度数
- A.30°
- B.60°
- C.90°
- D.30°或90°
D
分析:此题分为两种情况:当AD和AC在圆的同侧或当AD和AC在圆的两侧.连接BD,根据直径所对的圆周角是直角,得∠ADB=90°,运用锐角三角函数的知识求得∠BAD=60°,从而分别求得两种情况.
解答: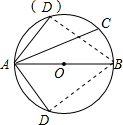 解:如图所示,连接BD.
解:如图所示,连接BD.
∵AB是⊙O直径,
∴∠ADB=90°.
∵AD=1,AB=2,
∴cos∠BAD= =
= ,
,
∴∠BAD=60°.
当AD和AC在圆的同侧时,则∠CAD=∠BAD-∠BAC=30°;
当AD和AC在圆的两侧时,则∠CAD=∠BAD+∠BAC=90°.
故选D.
点评:此题要考虑两种不同的情况,综合运用圆周角定理的推论和锐角三角函数的知识.
分析:此题分为两种情况:当AD和AC在圆的同侧或当AD和AC在圆的两侧.连接BD,根据直径所对的圆周角是直角,得∠ADB=90°,运用锐角三角函数的知识求得∠BAD=60°,从而分别求得两种情况.
解答:
 解:如图所示,连接BD.
解:如图所示,连接BD.∵AB是⊙O直径,
∴∠ADB=90°.
∵AD=1,AB=2,
∴cos∠BAD=
 =
= ,
,∴∠BAD=60°.
当AD和AC在圆的同侧时,则∠CAD=∠BAD-∠BAC=30°;
当AD和AC在圆的两侧时,则∠CAD=∠BAD+∠BAC=90°.
故选D.
点评:此题要考虑两种不同的情况,综合运用圆周角定理的推论和锐角三角函数的知识.

练习册系列答案
相关题目
已知AB是⊙O直径,AC是⊙O的弦,AB=2,∠BAC=30°,弦AD=1,那么∠CAD的度数( )
| A、30° | B、60° | C、90° | D、30°或90° |
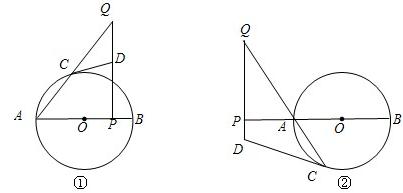
 如图,已知AB是⊙O直径,AC是⊙O弦,点D是
如图,已知AB是⊙O直径,AC是⊙O弦,点D是
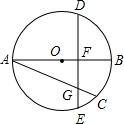
 (2013•德阳)如图,已知AB是⊙O直径,BC是⊙O的弦,弦ED⊥AB于点F,交BC于点G,过点C作⊙O的切线与ED的延长线交于点P.
(2013•德阳)如图,已知AB是⊙O直径,BC是⊙O的弦,弦ED⊥AB于点F,交BC于点G,过点C作⊙O的切线与ED的延长线交于点P. (2012•资阳)已知a、b是正实数,那么,
(2012•资阳)已知a、b是正实数,那么,