题目内容
函数y=
+
的最小值是（ ）
| x2-4x+5 |
| x2-4x+8 |
A、
| ||||
| B、3 | ||||
C、1+2
| ||||
| D、5 |
分析：化简函数，可得几何意义表示（x，0）与点（-2，1）、（2，2）两点间的距离的和，如图所示．利用两点之间，线段最短可以推知当点A、B、C三点共线时，点C到点A、B的距离之和最小，即AB=
=3．
| (-2-2)2+(1-2)2 |
解答：
解：y=
+
=
+
，
它表示（x，0）与点（2，-1）、（2，2）两点间的距离的和．
如图，当点A、B、C三点共线时，点C到点A、B的距离之和最小，即AB=
=3．
故选B．
解：y=| x2-4x+5 |
| x2-4x+8 |
| (x+2)2+(0+1)2 |
| (x-2)2+(0-2)2 |
它表示（x，0）与点（2，-1）、（2，2）两点间的距离的和．
如图，当点A、B、C三点共线时，点C到点A、B的距离之和最小，即AB=
| (-2-2)2+(1-2)2 |
故选B．
点评：本题考查了最短路线问题．此题需要学生具有一定的转化能力，属于基础题．
练习册系列答案
相关题目
，点N是x轴负半轴上的一点，NH⊥CM，交CM（或CM的延长线）于点H，交y轴于点D，且ND=CM．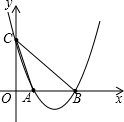
如图，已知二次函数y=x2-4x+3的图象交x轴于A、B两点（点A在点B的左侧）抛物线y=x2-4x+3交y轴于点C．