ĢāÄæÄŚČŻ
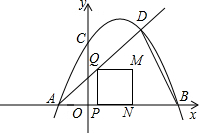 £Ø2012•¾°ÄžĻŲÄ£Äā£©ŅŃÖŖ¶ž“ĪŗÆŹży=-x2+4x+5Ķ¼Ļó½»xÖįÓŚµćA”¢B£¬½»yÖįÓŚµćC£¬µćDŹĒøĆŗÆŹżĶ¼ĻóÉĻŅ»µć£¬ĒŅµćDµÄŗį×ų±źĪŖ4£¬Į¬BD£¬µćPŹĒABÉĻŅ»¶Æµć£Ø²»ÓėµćAÖŲŗĻ£©£¬¹żP×÷PQ”ĶAB½»ÉäĻßADÓŚµćQ£¬ŅŌPQĪŖŅ»±ßŌŚPQµÄÓŅ²ą×÷Õż·½ŠĪPQMN£®ÉčµćPµÄ×ų±źĪŖ£Øt£¬0£©£®
£Ø2012•¾°ÄžĻŲÄ£Äā£©ŅŃÖŖ¶ž“ĪŗÆŹży=-x2+4x+5Ķ¼Ļó½»xÖįÓŚµćA”¢B£¬½»yÖįÓŚµćC£¬µćDŹĒøĆŗÆŹżĶ¼ĻóÉĻŅ»µć£¬ĒŅµćDµÄŗį×ų±źĪŖ4£¬Į¬BD£¬µćPŹĒABÉĻŅ»¶Æµć£Ø²»ÓėµćAÖŲŗĻ£©£¬¹żP×÷PQ”ĶAB½»ÉäĻßADÓŚµćQ£¬ŅŌPQĪŖŅ»±ßŌŚPQµÄÓŅ²ą×÷Õż·½ŠĪPQMN£®ÉčµćPµÄ×ų±źĪŖ£Øt£¬0£©£®£Ø1£©ĒóµćB£¬C£¬DµÄ×ų±ź¼°ÉäĻßADµÄ½āĪöŹ½£»
£Ø2£©ŌŚABÉĻŹĒ·ń“ęŌŚµćP£¬Ź¹”÷OCMĪŖµČŃüČż½ĒŠĪ£æČō“ęŌŚ£¬ĒóÕż·½ŠĪPQMN µÄ±ß³¤£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£»
£Ø3£©ÉčÕż·½ŠĪPQMNÓė”÷ABDÖŲµž²æ·ÖĆ껿ĪŖs£¬ĒósÓėtµÄŗÆŹż¹ŲĻµŹ½£®
·ÖĪö£ŗ£Ø1£©øł¾Ż¶ž“ĪŗÆŹż½āĪöŹ½£¬µ±x=0Ź±£¬Ēó³öCµć×ų±ź£»µ±y=0Ź±£¬Ēó³öBµć×ų±ź¼°µćA×ų±ź£»½«Dµćŗį×ų±ź“śČėy=-x2+4x+5£¬¼“æÉĒó³öµćDׯ×ų±ź£»øł¾ŻµćA”¢µćD×ų±ź£¬Ó¦ÓĆ“ż¶ØĻµŹż·Ø¼“æÉĒó³öÉäĻßAD½āĪöŹ½£»
£Ø2£©¼ŁÉč“ęŌŚµćP£¬Ź¹”÷OCMĪŖµČŃüČż½ĒŠĪ£¬øł¾Ż¹“¹É¶ØĄķ£¬ČōÄÜĒó³öPµć×ų±ź£¬ŌņP“ęŌŚ£¬Ķ¬Ź±æÉĒó³öÕż·½ŠĪPQMN µÄ±ß³¤£»·ńŌņP²»“ęŌŚ£»
£Ø3£©ÓÉÓŚÖŲµž²æ·ÖĆ껿ŹĒ²»Č·¶ØµÄ£¬ĖłŅŌŅŖøł¾ŻĘäÖŲµž³Ģ¶Č£¬·ÖĒéæöĢÖĀŪ£¬µĆµ½²»Ķ¬µÄ±ķ“ļŹ½£®
£Ø2£©¼ŁÉč“ęŌŚµćP£¬Ź¹”÷OCMĪŖµČŃüČż½ĒŠĪ£¬øł¾Ż¹“¹É¶ØĄķ£¬ČōÄÜĒó³öPµć×ų±ź£¬ŌņP“ęŌŚ£¬Ķ¬Ź±æÉĒó³öÕż·½ŠĪPQMN µÄ±ß³¤£»·ńŌņP²»“ęŌŚ£»
£Ø3£©ÓÉÓŚÖŲµž²æ·ÖĆ껿ŹĒ²»Č·¶ØµÄ£¬ĖłŅŌŅŖøł¾ŻĘäÖŲµž³Ģ¶Č£¬·ÖĒéæöĢÖĀŪ£¬µĆµ½²»Ķ¬µÄ±ķ“ļŹ½£®
½ā“š£ŗ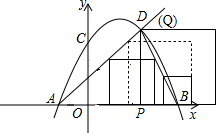 ½ā£ŗ£Ø1£©µ±x=0Ź±£¬y=5£¬ŌņCµć×ų±źĪŖ£Ø0£¬5£©£¬
½ā£ŗ£Ø1£©µ±x=0Ź±£¬y=5£¬ŌņCµć×ų±źĪŖ£Ø0£¬5£©£¬
µ±y=0Ź±£¬-x2+4x+5=0£¬
½āµĆ£Øx+1£©£Øx-5£©=0£¬
x1=-1£»x2=5£®
ŌņAµć×ų±źĪŖ£Ø-1£¬0£©£¬Bµć×ų±źĪŖ£Ø5£¬0£©£®
½«x=4“śČėy=-x2+4x+5µĆ£¬y=-16+16+5=5£¬
ŌņDµć×ų±źĪŖ£Ø4£¬5£©£®
ÉčADµÄ½āĪöŹ½ĪŖy=kx+b£¬
°ŃA£Ø-1£¬0£©£¬D£Ø4£¬5£©·Ö±š“śČė½āĪöŹ½y=kx+bµĆ£¬
£¬
½āµĆ
£¬
ŗÆŹż½āĪöŹ½ĪŖy=x+1£Øx”Ż-1£©£®£Ø2·Ö£©
£Ø2£©”ßÖ±ĻßADµÄ½āĪöŹ½ĪŖ£ŗy=x+1£¬ĒŅP£Øt£¬0£©£®
”ąQ£Øt£¬t+1£©£¬M£Ø2t+1£¬t+1£©
µ±MC=MOŹ±£ŗt+1=
£¬
”ą±ß³¤ĪŖ
£®”£Ø1·Ö£©
µ±OC=OMŹ±£ŗ£Ø2t+1£©2+£Øt+1£©2=52
½āµĆt1=-
-
£ØÉįČ„£©£¬t1=-
+
”ą±ß³¤ĪŖt+1=
+
£®”£Ø2·Ö£©
µ±CO=CMŹ±£ŗ£Ø2t+1£©2+£Ø4-t£©2=52
½āµĆt1=
£¬t2=
£®
”ą±ß³¤ĪŖt+1=
£®
»ņt+1=t2=
”£Ø2·Ö£©
£Ø3£©µ±1£¼t”Ü
Ź±£¬Õż·½ŠĪµÄ±ß³¤ĪŖ£Øt+1£©£¬¹ŹĘäĆ껿ĪŖ£ŗs=£Øt+1£©2£»”£Ø1·Ö£©
µ±
”Üt”Ü2Ź±£ŗs=-
t2+
t-
£»”£Ø1·Ö£©
µ±2”Üt”Ü4Ź±£ŗs=-
t2+
t+
£»”£Ø1·Ö£©
µ±4”Üt”Ü5Ź±£ŗs=
t2-25t+
£®”£Ø1·Ö£©
 ½ā£ŗ£Ø1£©µ±x=0Ź±£¬y=5£¬ŌņCµć×ų±źĪŖ£Ø0£¬5£©£¬
½ā£ŗ£Ø1£©µ±x=0Ź±£¬y=5£¬ŌņCµć×ų±źĪŖ£Ø0£¬5£©£¬µ±y=0Ź±£¬-x2+4x+5=0£¬
½āµĆ£Øx+1£©£Øx-5£©=0£¬
x1=-1£»x2=5£®
ŌņAµć×ų±źĪŖ£Ø-1£¬0£©£¬Bµć×ų±źĪŖ£Ø5£¬0£©£®
½«x=4“śČėy=-x2+4x+5µĆ£¬y=-16+16+5=5£¬
ŌņDµć×ų±źĪŖ£Ø4£¬5£©£®
ÉčADµÄ½āĪöŹ½ĪŖy=kx+b£¬
°ŃA£Ø-1£¬0£©£¬D£Ø4£¬5£©·Ö±š“śČė½āĪöŹ½y=kx+bµĆ£¬
|
½āµĆ
|
ŗÆŹż½āĪöŹ½ĪŖy=x+1£Øx”Ż-1£©£®£Ø2·Ö£©
£Ø2£©”ßÖ±ĻßADµÄ½āĪöŹ½ĪŖ£ŗy=x+1£¬ĒŅP£Øt£¬0£©£®
”ąQ£Øt£¬t+1£©£¬M£Ø2t+1£¬t+1£©
µ±MC=MOŹ±£ŗt+1=
| 5 |
| 2 |
”ą±ß³¤ĪŖ
| 5 |
| 2 |
µ±OC=OMŹ±£ŗ£Ø2t+1£©2+£Øt+1£©2=52
½āµĆt1=-
| 3 |
| 5 |
2
| ||
| 5 |
| 3 |
| 5 |
2
| ||
| 5 |
”ą±ß³¤ĪŖt+1=
| 2 |
| 5 |
2
| ||
| 5 |
µ±CO=CMŹ±£ŗ£Ø2t+1£©2+£Ø4-t£©2=52
½āµĆt1=
2+2
| ||
| 5 |
2-2
| ||
| 5 |
”ą±ß³¤ĪŖt+1=
7+2
| ||
| 5 |
»ņt+1=t2=
7-2
| ||
| 5 |
£Ø3£©µ±1£¼t”Ü
| 19 |
| 11 |
µ±
| 19 |
| 11 |
| 111 |
| 10 |
| 219 |
| 5 |
| 351 |
| 5 |
µ±2”Üt”Ü4Ź±£ŗs=-
| 11 |
| 10 |
| 19 |
| 5 |
| 49 |
| 10 |
µ±4”Üt”Ü5Ź±£ŗs=
| 5 |
| 2 |
| 125 |
| 2 |
µćĘĄ£ŗ±¾Ģāæ¼²éĮĖ¶ž“ĪŗÆŹżµÄĶ¼ĻóŗĶŠŌÖŹ”¢“ż¶ØĻµŹż·ØĒóŅ»“ĪŗÆŹż½āĪöŹ½”¢Čż½ĒŠĪ¼°Õż·½ŠĪµÄŠŌÖŹ”¢“ęŌŚŠŌĪŹĢāµČÄŚČŻ£¬×ŪŗĻŠŌĒ棬ŹōÓŚÄŃĢā£®

Į·Ļ°²įĻµĮŠ“š°ø
Ļą¹ŲĢāÄæ
 £Ø2012•¾°ÄžĻŲÄ£Äā£©ČēĶ¼ĖłŹ¾£¬Ä³ŹŠµÄA”¢BĮ½µŲĻą¾ą20km£¬BŌŚAµÄ±±Ę«¶«45”ć·½ĻņÉĻ£¬Ņ»øߊĀ¼¼ŹõŌ°ĒųPŌŚAµÄ±±Ę«¶«30”ćŗĶBµÄÕżĪ÷·½ĻņÉĻ£®ĻÖ¼Ę»®ŠŽ½ØµÄŅ»ĢõøßĖŁĢśĀ·½«¾¹żAB£ØĻ߶Ī£©£¬ŅŃÖŖøߊĀ¼¼ŹõŌ°ĒųµÄ·¶Ī§ŌŚŅŌµćPĪŖŌ²ŠÄ£¬°ė¾¶ĪŖ4kmµÄŌ²ŠĪĒųÓņÄŚ£®ĒėĶعż¼ĘĖć»Ų“š£ŗÕāĢõøßĖŁĢśĀ·»į²»»į“©Ō½øߊĀ¼¼ŹõŌ°Ēų£æ£Ø²Īæ¼Źż¾Ż£ŗsin15”ć”Ö0.2588£¬cos15”ć”Ö0.9659£¬tan15”ć”Ö0.2679£©£®
£Ø2012•¾°ÄžĻŲÄ£Äā£©ČēĶ¼ĖłŹ¾£¬Ä³ŹŠµÄA”¢BĮ½µŲĻą¾ą20km£¬BŌŚAµÄ±±Ę«¶«45”ć·½ĻņÉĻ£¬Ņ»øߊĀ¼¼ŹõŌ°ĒųPŌŚAµÄ±±Ę«¶«30”ćŗĶBµÄÕżĪ÷·½ĻņÉĻ£®ĻÖ¼Ę»®ŠŽ½ØµÄŅ»ĢõøßĖŁĢśĀ·½«¾¹żAB£ØĻ߶Ī£©£¬ŅŃÖŖøߊĀ¼¼ŹõŌ°ĒųµÄ·¶Ī§ŌŚŅŌµćPĪŖŌ²ŠÄ£¬°ė¾¶ĪŖ4kmµÄŌ²ŠĪĒųÓņÄŚ£®ĒėĶعż¼ĘĖć»Ų“š£ŗÕāĢõøßĖŁĢśĀ·»į²»»į“©Ō½øߊĀ¼¼ŹõŌ°Ēų£æ£Ø²Īæ¼Źż¾Ż£ŗsin15”ć”Ö0.2588£¬cos15”ć”Ö0.9659£¬tan15”ć”Ö0.2679£©£®