题目内容
【题目】已知双曲线y=
（x＞0），直线l1：y﹣
=k（x﹣）（k＜0）过定点F且与双曲线交于A，B两点，设A（x1 ， y1），B（x2 ， y2）（x1＜x2），直线l2：y=﹣x+ ．
（1）若k=﹣1，求△OAB的面积S；
（2）
若AB=
， 求k的值；
（3）设N（0，2），P在双曲线上，M在直线l2上且PM∥x轴，求PM+PN最小值，并求PM+PN取得最小值时P的坐标．
（参考公式：在平面直角坐标系中，若A（x1 ， y1），B（x2 ， y2）则A，B两点间的距离为AB=
）
【答案】
（1）
解：当k=-1时，l1：y=﹣x+2
，
联立得，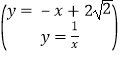
，化简得x2﹣2x+1=0，
解得：x1=﹣1，x2=+1，
设直线l1与y轴交于点C，则C（0，2）．
S△OAB=S△AOC﹣S△BOC=
2（x2﹣x1）=2；
（2）
解：根据题意得：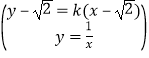
整理得：kx2+（1﹣k）x﹣1=0（k＜0），
∵△=[（1﹣k）]2﹣4×k×（﹣1）=2（1+k2）＞0，
∴x1、x2 是方程的两根，
∴
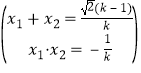①，
∴AB=
=
=
=
，
将①代入得，AB=
=
（k＜0），
∴=
，
整理得：2k2+5k+2=0，
解得：k=﹣2，或 k=；
（3）
解：∵直线l1：y﹣=k（x﹣）（k＜0）过定点F,
∴ F（，）.
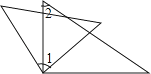
如图：
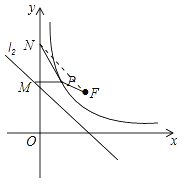
设P（x，
），则M（﹣+，），
则PM=x+﹣=
=
，
∵PF=
=，
∴PM=PF．
∴PM+PN=PF+PN≥NF=2，
当点P在NF上时等号成立，此时NF的方程为y=﹣x+2，
由（1）知P（﹣1，+1），
∴当P（﹣1，+1）时，PM+PN最小值是2．
【解析】（1）将l1与y=组成方程组，即可得到C点坐标，从而求出△OAB的面积；
（2）根据题意得：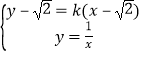
整理得：kx2+（1﹣k）x﹣1=0（k＜0），根据根与系数的关系得到2k2+5k+2=0，从而求出k的值；
（3）设P（x，），则M（﹣+ ， ），根据PM=PF，求出点P的坐标．
