题目内容
已知二次函数y=ax2+bx+c的图象经过A(2,4),其顶点的横坐标是| 1 | 2 |
(1)此函数的解析式,并画出图象;
(2)在x轴上方的图象上是否存在着D,使S△ABC=2S△DBC?若存在,求出D的值;若不存在,说明理由.
分析:(1)已知函数的解析式,把点(2,4)代入,然后再根据顶点坐标公式及方程两根之和和两根之差,列出三个式子,从而求解;
(2)先设出D点的坐标,然后再根据已知条件S△ABC=2S△DBC,求出D点的坐标,从而求解.
(2)先设出D点的坐标,然后再根据已知条件S△ABC=2S△DBC,求出D点的坐标,从而求解.
解答: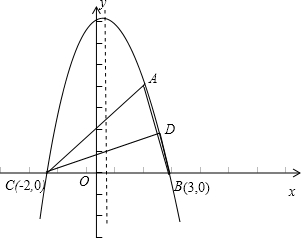 解:(1)∵二次函数y=ax2+bx+c的图象经过A(2,4),
解:(1)∵二次函数y=ax2+bx+c的图象经过A(2,4),
∴4a+2b+c=4 ①
∵顶点的横坐标是
,
-
=
②
∵函数图象与x轴交点为B(x1,0)和(x2,0),
∴x1+x2=-
,x1x2=
,
∴x12+x22=(x1+x2)2-2x1x2=
=13③
x12+x22=(x1+x2)2-2x1x2,
由②得:a=-b代入①得:-2b+c=4 c=2b+4,
将a=-b c=2b+4代入③得:b2+2b(2b+4)=13b2,
b=0或b=1
∵b=0不合题意,
∴b=1,a=-1,c=6
∴y=-x2+x+6;
(2)设D(x,y) 则S△ABC=
×BC×4=10,
S△DBC=
×5|y|=
y=5,
∴y=2,
将y=2代入y=-x2+x+6,
x=
∴D(
,2)或(
,2).
 解:(1)∵二次函数y=ax2+bx+c的图象经过A(2,4),
解:(1)∵二次函数y=ax2+bx+c的图象经过A(2,4),∴4a+2b+c=4 ①
∵顶点的横坐标是
| 1 |
| 2 |
-
| b |
| 2a |
| 1 |
| 2 |
∵函数图象与x轴交点为B(x1,0)和(x2,0),
∴x1+x2=-
| b |
| a |
| c |
| a |
∴x12+x22=(x1+x2)2-2x1x2=
| b2-2ac |
| a2 |
x12+x22=(x1+x2)2-2x1x2,
由②得:a=-b代入①得:-2b+c=4 c=2b+4,
将a=-b c=2b+4代入③得:b2+2b(2b+4)=13b2,
b=0或b=1
∵b=0不合题意,
∴b=1,a=-1,c=6
∴y=-x2+x+6;
(2)设D(x,y) 则S△ABC=
| 1 |
| 2 |
S△DBC=
| 1 |
| 2 |
| 5 |
| 2 |
∴y=2,
将y=2代入y=-x2+x+6,
x=
1±
| ||
| 2 |
∴D(
1+
| ||
| 2 |
1-
| ||
| 2 |
点评:(1)第一问主要考查了用待定系数法求函数的解析式,还考查一元二次方程与函数的关系.
(2)此问把三角形的面积公式同函数结合起来出题,求特殊点的坐标,比较新颖.
(2)此问把三角形的面积公式同函数结合起来出题,求特殊点的坐标,比较新颖.

练习册系列答案
相关题目
已知二次函数y=ax+bx+c(a≠0,a,b,c为常数),对称轴为直线x=1,它的部分自变量与函数值y的对应值如下表,写出方程ax2+bx+c=0的一个正数解的近似值________(精确到0.1).
| x | -0.1 | -0.2 | -0.3 | -0.4 |
| y=ax2+bx+c | -0.58 | -0.12 | 0.38 | 0.92 |
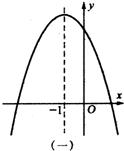 21、已知二次函数y=a(x+1)2+c的图象如图所示,则函数y=ax+c的图象只可能是( )
21、已知二次函数y=a(x+1)2+c的图象如图所示,则函数y=ax+c的图象只可能是( )
