题目内容
 如图,依次摆放着七个正方形,已知斜放置的三个三角形的面积分别为1、2、3,正放着的四个正方形的面积依次是S1、S2、S3、S4,则S1+S2+S3+S4=
如图,依次摆放着七个正方形,已知斜放置的三个三角形的面积分别为1、2、3,正放着的四个正方形的面积依次是S1、S2、S3、S4,则S1+S2+S3+S4=4
4
.分析:如图,易证△ABC≌△CDE,得AB2+DE2=DE2+CD2=CE2,同理FG2+LK2=HL2,S1+S2+S3+S4=1+3=4.
解答: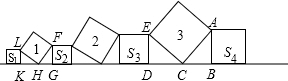 解:
解:
∵依次摆放着七个正方形,
∴EC=AC,∠EDC=∠ABC=∠ECA=90°,
∴∠ECD+∠ACB=90°,∠ECD+∠DEC=90°,
∴∠ECD=∠CAB,∠ACB=∠CED,
在△ABC和△CDE中,
∵
,
∴△ABC≌△CDE,
∴AB=CD,BC=DE,
∴AB2+DE2=DE2+CD2=CE2=3,
同理可证FG2+LK2=HL2=1,
∴S1+S2+S3+S4=CE2+HL2=1+3=4.
故答案为:4.
 解:
解:∵依次摆放着七个正方形,
∴EC=AC,∠EDC=∠ABC=∠ECA=90°,
∴∠ECD+∠ACB=90°,∠ECD+∠DEC=90°,
∴∠ECD=∠CAB,∠ACB=∠CED,
在△ABC和△CDE中,
∵
|
∴△ABC≌△CDE,
∴AB=CD,BC=DE,
∴AB2+DE2=DE2+CD2=CE2=3,
同理可证FG2+LK2=HL2=1,
∴S1+S2+S3+S4=CE2+HL2=1+3=4.
故答案为:4.
点评:本题考查了全等三角形的证明,考查了勾股定理的灵活运用,本题中证明AB2+DE2=DE2+CD2=CE2是解题的关键.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目

 如图,依次摆放着七个正方形,已知斜放置的三个三角形的面积分别为1、2、3,正放着的四个正方形的面积依次是S1、S2、S3、S4,则S1+S2+S3+S4=________.
如图,依次摆放着七个正方形,已知斜放置的三个三角形的面积分别为1、2、3,正放着的四个正方形的面积依次是S1、S2、S3、S4,则S1+S2+S3+S4=________.