题目内容
.阅读材料:如图9,在平面直角坐标系中,![]() 、
、![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,
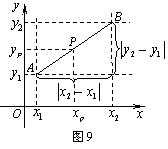
![]() ,
,![]() 中点
中点![]() 的坐标为
的坐标为![]() .由
.由![]() ,得
,得![]() ,
,
同理![]() ,所以
,所以![]() 的中点坐标为
的中点坐标为![]() .
.
由勾股定理得![]() ,所以
,所以![]() 、
、![]() 两点
两点
间的距离公式为![]() .
.
注:上述公式对![]() 、
、![]() 在平面直角坐标系中其它位置也成立.
在平面直角坐标系中其它位置也成立.
解答下列问题:
如图10,直线![]() :
:![]() 与抛物线
与抛物线![]() 交于
交于![]() 、
、![]() 两点,
两点,![]() 为
为![]() 的中点,
的中点,
过![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() .
.
(1)求![]() 、
、![]() 两点的坐标及
两点的坐标及![]() 点的坐标;
点的坐标;
(2)连结![]() ,求证
,求证![]() 为直角三角形;
为直角三角形;
(3)将直线![]() 平移到
平移到![]() 点时得到直线
点时得到直线![]() ,求两
,求两
直线![]() 与
与![]() 的距离.
的距离.
 |
.
解:(1)由![]() ,解得
,解得 ,
, .
.
则![]() ,
,![]() 两点的坐标分别为:
两点的坐标分别为:![]() ,
,![]() ,
,
∵![]() 是
是![]() ,
,![]() 的中点,由中点坐标公式得
的中点,由中点坐标公式得![]() 点坐标为
点坐标为![]() ,
,
又![]() 轴交抛物线于
轴交抛物线于![]() 点,将
点,将![]() 代入
代入![]() 中得
中得![]() ,
,
∴![]() 点坐标为
点坐标为![]() .
.
(2)由两点间距离公式得:
![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,即
,即![]()
∴ ![]() 为直角三角形.
为直角三角形.
(3)过点![]() 作
作![]() 于
于![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,
,
则![]() 点的坐标为
点的坐标为![]() ,
,
∴ ![]() ,
,
∴![]() .
.
又直线![]() 与
与![]() 之间的距离等于点C到
之间的距离等于点C到![]() 的距离CG,
的距离CG,
∴直线![]() 与
与![]() 之间的距离为
之间的距离为![]() .
.
 |

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目


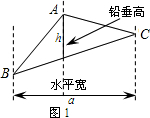 阅读材料:
阅读材料: