题目内容
如图，四边形
为正方形，点
在
轴上，点
在
轴上，且
，
，反比例函数
在第一象限的图像经过正方形的顶点
．
（1）求反比例函数的关系式；
（2）将正方形沿轴向左平移 个单位长度时，点
恰好落在反比例函数的图像上．
【答案】
（1）
（2）2
【解析】解:（1）过点
作
⊥
轴于点
．
则
………………（1分）
∵四边形
为正方形
∴
，
………………（3分）
∴
∵
∴
∴△
≌△
………………（4分）
∴
，
，
∴
∴点的坐标为（6，2）
把（6，2）代入
得：
, 解得：
∴所求的反比例函数关系式为………………（7分）
（2）将正方形沿轴向左平移 2 个单位长度时，点
恰好落
在反比例函数的图像上.…………………………（9分）
（1）过点作⊥轴于点，证得△≌△，可求出点的坐标，从而求得反比例函数关系式
（2）将正方形沿轴向左平移 2 个单位长度时，点恰好落
在反比例函数的图像上
练习册系列答案
相关题目
同时，点R从O出发沿OM方向以
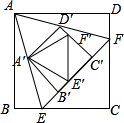内接正方形，△A′E′F′为正方形A′B′C′D′的内接正三角形．
如图，P为正方形ABCD内的一点，画?PAHD，?PBEA，?PCFB，?PDGC，请证明：以E，F，G，H为顶点的四边形是正方形．
为正方形，点
在
轴上，点
在
轴上，且
，
，反比例函数
在第一象限的图像经过正方形的顶点
．
恰好落在反比例函数的图像上．