Question

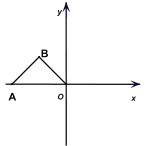
【题目】如图所示，在直角坐标系中，等腰直角的顶点是坐标原点，点的坐标是，直角顶点在第二象限，把绕点旋转到，点与对应，点与对应，那么点的坐标是_________．

Answer 1

【答案】或

【解析】

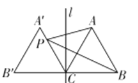
根据△AOB绕点O旋转15°得到△A'OB'，分两种情况，过B'作B'C⊥y轴，依据Rt△B'OC中，B'C和CO的长，即可得到点B'的坐标．

解：如图所示：若△AOB绕点O顺时针旋转15°得到△A'OB'，过B'作B'C⊥y轴，则∠BOB'=15°，

又∵∠AOB=45°，
∴∠BOC=45°，
∴∠B'OC=30°，
∵点A的坐标是（-4，0），
∴AO=4，
∴B'O=BO=cos45°×4=2，
∴B'C=B'O=，CO=B'C=，
∴点B'的坐标是；
如图所示：若△AOB绕点O逆时针旋转15°得到△A'OB'，过B'作B'C⊥y轴，则∠BOB'=15°，

同理可得，∠AOB'=30°，B'O=2，
∴∠CB'O=30°，
∴CO=B'O=，B'C=CO=，
∴点B'的坐标是，
综上所述，点B'的坐标是或．
故答案为：或．