题目内容
1.若不等式组$\left\{\begin{array}{l}{x+a>0}\\{1-2x>x-2}\end{array}\right.$无解,则a的取值范围是( )| A. | a≤-1 | B. | a<-1 | C. | a≥1 | D. | a>1 |
分析 根据解不等式的方法可以分别求得各个不等式的解集,再根据不等式组无解,从而可以求得a的取值范围.
解答 解:$\left\{\begin{array}{l}{x+a>0}&{①}\\{1-2x>x-2}&{②}\end{array}\right.$,
由不等式①,得x>-a,
由不等式②,得x<1,
∵不等式组$\left\{\begin{array}{l}{x+a>0}\\{1-2x>x-2}\end{array}\right.$无解,
∴-a≥1,
解得,a≤-1,
故选A.
点评 本题考查解一元一次不等式组,解答本题的关键是明确解一元一次不等式的方法.

练习册系列答案
相关题目
9.正方形具有而矩形不一定具有的性质是( )
| A. | 四个角都为直角 | B. | 对角线互相平分 | C. | 对角线相等 | D. | 对角线互相垂直 |
6.甲、乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字的个数经统计计算后填入下表:
某同学根据上表分析得出如下结论:①甲、乙两班学生成绩的平均水平相同;②乙班优秀人数多于甲班优秀人数(每分钟输入汉字数≥150个为优秀);③甲班的成绩波动比乙班的成绩波动大,上述结论正确的是①②③.
| 班级 | 参赛人数 | 平均字数 | 中位数 | 方差 |
| 甲 | 55 | 135 | 149 | 191 |
| 乙 | 55 | 135 | 151 | 110 |
13.计算a2•a4的结果是( )
| A. | a6 | B. | 2a6 | C. | a8 | D. | 2a8 |
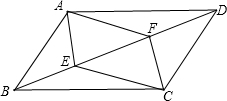 如图,在四边形ABCD中,AB∥CD,AD∥BC,现在请你添加一个适当的条件:BE=DF,使得四边形AECF为平行四边形(图中不再添加点和线).
如图,在四边形ABCD中,AB∥CD,AD∥BC,现在请你添加一个适当的条件:BE=DF,使得四边形AECF为平行四边形(图中不再添加点和线).


