题目内容
方程||x-3|+3x|=1的解是分析:把方程||x-3|+3x|=1从外到内依次去绝对值后即可解答.
解答:解:∵||x-3|+3x|=1,
∴|x-3|+3x=1或|x-3|+3x=-1,
①当|x-3|+3x=1时,可化为:x-3=1-3x或-x+3=1-3x,1-3x≥0?x≤
,
解得:x=1舍去,x=-1符合题意;
②当|x-3|+3x=-1时,可化为:x-3=-1-3x或x-3=1+3x,1+3x≤0?x≤-
,
解得:x=
舍去,x=-2符合题意;
综上所述:x=-2或-1.
故答案为:-2或-1.
∴|x-3|+3x=1或|x-3|+3x=-1,
①当|x-3|+3x=1时,可化为:x-3=1-3x或-x+3=1-3x,1-3x≥0?x≤
| 1 |
| 3 |
解得:x=1舍去,x=-1符合题意;
②当|x-3|+3x=-1时,可化为:x-3=-1-3x或x-3=1+3x,1+3x≤0?x≤-
| 1 |
| 3 |
解得:x=
| 1 |
| 2 |
综上所述:x=-2或-1.
故答案为:-2或-1.
点评:本题考查了含绝对值符号的一元一次方程,属于基础题,关键是正确去绝对值符号.

练习册系列答案
相关题目
下列方程中,以x表示y的是( )
| A、x+y=8 | ||
B、x=
| ||
| C、2y=5x+7 | ||
| D、y=2x-1 |
关于x的分式方程
=
无解,则m的值为( )
| 2x |
| x+1 |
| m |
| x+1 |
| A、-2 | B、-1 | C、0 | D、2 |
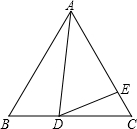 已知:等边△ABC中,AB、cosB是关于x的方程x2-4mx-
已知:等边△ABC中,AB、cosB是关于x的方程x2-4mx-