题目内容
已知抛物线y=ax2+bx+c(a>0)经过A(-9,-5),而且b=6a,求出抛物线y=ax2+bx+c(a>0)经过的另一个定点(点A除外,定点坐标为常数).
考点:二次函数图象上点的坐标特征
专题:计算题
分析:根据二次函数图象上点的坐标特征得到81a-9b+c=-5,把b=6a代入可用a表示c得到c=-27a-5,则抛物线解析式变形为y=ax2+6ax-27a-5,再变形为关于a的方程(x2+6x-27)a=y+5,利用不定方程的解法得到x2+6x-27=0,y+5=0,解得x=-9,y=-5或x=3,y=5,于是可确定抛物线y=ax2+bx+c(a>0)经过的另一个定点坐标.
解答:解:∵A(-9,-5)在抛物线y=ax2+bx+c上,
∴81a-9b+c=-5,
而b=6a,
∴81a-54a+c=-5,
∴c=-27a-5,
∴y=ax2+6ax-27a-5,
∴(x2+6x-27)a=y+5,
∵a>0的任意数,
∴x2+6x-27=0,y+5=0,
∴x=-9,y=-5或x=3,y=5,
∴抛物线y=ax2+bx+c(a>0)经过的另一个定点坐标为(3,5).
∴81a-9b+c=-5,
而b=6a,
∴81a-54a+c=-5,
∴c=-27a-5,
∴y=ax2+6ax-27a-5,
∴(x2+6x-27)a=y+5,
∵a>0的任意数,
∴x2+6x-27=0,y+5=0,
∴x=-9,y=-5或x=3,y=5,
∴抛物线y=ax2+bx+c(a>0)经过的另一个定点坐标为(3,5).
点评:本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了解不定方程.

练习册系列答案
相关题目
 如图,∠BAC=45°,BD:DC:BC=3:4:5,AD=4,∠ABC+∠ABD=180°,∠ACB+∠ACD=180°,求四边形ABCD的面积.
如图,∠BAC=45°,BD:DC:BC=3:4:5,AD=4,∠ABC+∠ABD=180°,∠ACB+∠ACD=180°,求四边形ABCD的面积.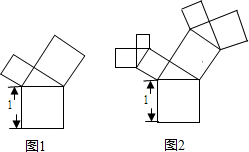 有一个边长为1的正方形,经过一次“生长”后在它的上侧生长出两个小正方形(如图1),且三个正方形所围成的三角形是直角三角形;再经过一次“生长”后变成了图2,如此继续“生长”下去,则“生长”第k次后所有正方形的面积和为( )
有一个边长为1的正方形,经过一次“生长”后在它的上侧生长出两个小正方形(如图1),且三个正方形所围成的三角形是直角三角形;再经过一次“生长”后变成了图2,如此继续“生长”下去,则“生长”第k次后所有正方形的面积和为( )