题目内容
 如图,△ACD、△ABE、△BCF均为直线BC同侧的等边三角形.当AB≠AC时,求证:四边形ADFE为平行四边形.
如图,△ACD、△ABE、△BCF均为直线BC同侧的等边三角形.当AB≠AC时,求证:四边形ADFE为平行四边形.
证明:
∵△ABE、△BCF为等边三角形,
∴AB=BE=AE,BC=CF=FB,∠ABE=∠CBF=60°.
∴∠FBE=∠CBA,
在△FBE和△CBA中,
 ,
,
∴△FBE≌△CBA(SAS).
∴EF=AC.
又∵△ADC为等边三角形,
∴CD=AD=AC.
∴EF=AD.
同理可得AE=DF.
∴四边形AEFD是平行四边形.
分析:根据等边三角形的性质得出边角之间的关系,再利用全等三角形的判定得出△FBE≌△CBA,进而得出EF=AD,同理可得AE=DF,即可得出四边形ADFE为平行四边形.
点评:此题主要考查了全等三角形的判定与性质以及平行四边形的判定,得出EF=AD是解题关键.
∵△ABE、△BCF为等边三角形,
∴AB=BE=AE,BC=CF=FB,∠ABE=∠CBF=60°.
∴∠FBE=∠CBA,
在△FBE和△CBA中,
 ,
,∴△FBE≌△CBA(SAS).
∴EF=AC.
又∵△ADC为等边三角形,
∴CD=AD=AC.
∴EF=AD.
同理可得AE=DF.
∴四边形AEFD是平行四边形.
分析:根据等边三角形的性质得出边角之间的关系,再利用全等三角形的判定得出△FBE≌△CBA,进而得出EF=AD,同理可得AE=DF,即可得出四边形ADFE为平行四边形.
点评:此题主要考查了全等三角形的判定与性质以及平行四边形的判定,得出EF=AD是解题关键.

练习册系列答案
相关题目
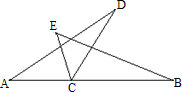 5、如图,△ACD≌△ECB,A,C,B在一条直线上,且A和E是一对对应顶点,如果∠BCE=130°,那么将△ACD围绕C点顺时针旋转( )与△ECB重合.
5、如图,△ACD≌△ECB,A,C,B在一条直线上,且A和E是一对对应顶点,如果∠BCE=130°,那么将△ACD围绕C点顺时针旋转( )与△ECB重合. 21、如图,∠ACD是△ABC的一个外角,请你从下面三个条件中,选出两个作为已知条件,另一个作为结论,推出一个正确的命题.
21、如图,∠ACD是△ABC的一个外角,请你从下面三个条件中,选出两个作为已知条件,另一个作为结论,推出一个正确的命题.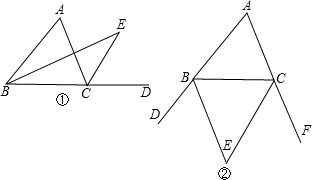
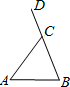 (2011•安宁市一模)如图,∠ACD是等腰△ABC的一个外角,已知AB=AC,∠A=50°,那么∠ACD=( )
(2011•安宁市一模)如图,∠ACD是等腰△ABC的一个外角,已知AB=AC,∠A=50°,那么∠ACD=( ) 如图,∠ACD是△ABC的外角,∠A=50°,∠ACD=110°,
如图,∠ACD是△ABC的外角,∠A=50°,∠ACD=110°,