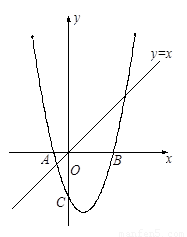题目内容
如图1,已知抛物线 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB =" 2OA" = 4.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB =" 2OA" = 4.

(1)求该抛物线的函数表达式;
(2)设P是(1)中抛物线上的一个动点,以P为圆心,R为半径作⊙P,求当⊙P与抛物线的对称轴l及x轴均相切时点P的坐标.
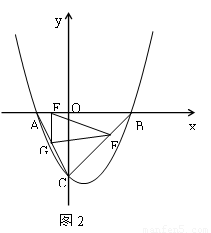
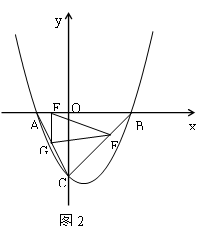
(3)动点E从点A出发,以每秒1个单位长度的速度向终点B运动,动点F从点B出发,以每秒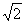 个单位长度的速度向终点C运动,过点E作EG//y轴,交AC于点G(如图2).若E、F两点同时出发,运动时间为t.则当t为何值时,△EFG的面积是△ABC的面积的
个单位长度的速度向终点C运动,过点E作EG//y轴,交AC于点G(如图2).若E、F两点同时出发,运动时间为t.则当t为何值时,△EFG的面积是△ABC的面积的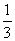 ?
?
(1)抛物线为 (2)满足条件的点P的坐标为P1(
(2)满足条件的点P的坐标为P1(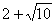 ,
, )、P2(
)、P2(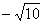 ,
, )、P3(
)、P3( ,
, )、P4(
)、P4(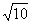 ,
, )(3)当t = 1时,△EFG的面积是△ABC的面积的
)(3)当t = 1时,△EFG的面积是△ABC的面积的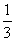
【解析】
试题分析:(1)解:∵OB=2OA=4
∴A(–2,0)、B(4,0)
由已知得:

解得: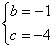
所求抛物线为
(2)解法一:当点P在第一象限时,
过点P作PQ⊥l于Q,作PR⊥x轴于R
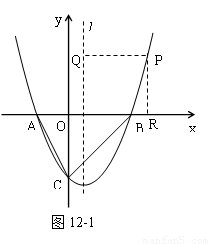
⊙P与x轴、直线l都相切,
∴PQ=PR
由(1)知抛物线的对称轴l为x = 1,设P(x,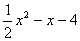 )
)
则PQ = x–1,PR = 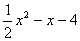
∴x–1 = 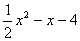 ,解得:
,解得: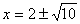 (其中
(其中 舍去)
舍去)
∴PR =" PQ" = x–1=
∴P(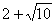 ,
, )
)
同理,当点P在第二象限时,可得P(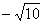 ,
, )
)
当点P在第三象限时,可得P( ,
, )
)
当点P在第四象限时,可得P(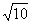 ,
, )
)
综上述,满足条件的点P的坐标为P1(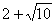 ,
, )、P2(
)、P2(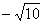 ,
, )、P3(
)、P3( ,
, )、P4(
)、P4(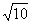 ,
, )
)
解法二:由已知得点P也在由对称轴l及x轴所组成的角的平分线所在的直线m上

当直线m过一、三、四象限时,设直线m与y轴交于N,对称轴l与x轴交于M
由(1)知直线l为x = 1
故M(1,0)
∵∠OMN =45º=∠ONM
∴ON =" OM" = 1
∴N(0,–1)
∴直线m为:y = x–1
解方程组
得:

∴点P的坐标为(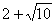 ,
, )或(
)或( ,
, )
)
当直线m经过一、二、四象限时,
同理可得点P的坐标为(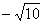 ,
, )或(
)或(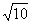 ,
, )
)
∴点P的坐标为P1(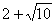 ,
, )、P2(
)、P2(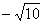 ,
, )、P3(
)、P3( ,
, )、P4(
)、P4(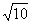 ,
, )
)
(3)解:过点F作FH⊥EG于点H,作FJ⊥x轴于J
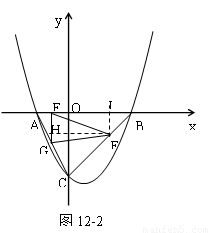
由(1)知点C的坐标为(0,–4)
∴OB=OC=4
∵∠OBC=∠OCB = 45º
∴FJ=BJ=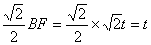
∴F(4–t,t)
∵AE = t,∴E(–2 + t,0)
∴A(–2,0)、C(0,–4)
∴直线AC为:y =–2x–4
把x =–2 + t代入得:y =–2t,∴G(–2 + t,–2t)
∴EG = 2t,FH = (4–t )–(–2 + t ) = 6–2t
∴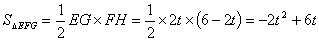
∵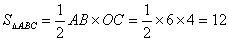
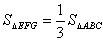
∴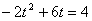 ,解得
,解得 ,
,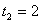
∵当t = 2时,G(0,–4),E(0,0),此时EG与OC重合,不合题意,舍去
∴当t = 1时,△EFG的面积是△ABC的面积的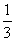 .
.
考点:二次函数和动点问题
点评:本题难度较大,主要考查学生对二次函数解决动点问题综合运用能力,动点为中考常考题型,要求学生注意培养数形结合思想,培养综合分析归纳能力,并运用到考试中去。

 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
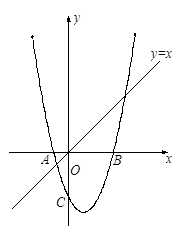
 与x 轴交于两点A、B,其顶点为C.
与x 轴交于两点A、B,其顶点为C.
 平行四边形?若存在,求点P的坐标;若不存在,请说明理由.
平行四边形?若存在,求点P的坐标;若不存在,请说明理由.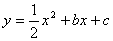 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB =" 2OA" = 4.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB =" 2OA" = 4.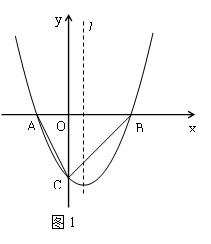
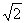 个单位长度的速度向终点C运动,过点E作EG//y轴,交AC于点G(如图2).若E、F两点同时出发,运动时间为t.则当t为何值时,△EFG的面积是△ABC的面积的
个单位长度的速度向终点C运动,过点E作EG//y轴,交AC于点G(如图2).若E、F两点同时出发,运动时间为t.则当t为何值时,△EFG的面积是△ABC的面积的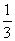 ?
?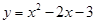 与x轴交于点A和点B,与y轴相交于点C.
与x轴交于点A和点B,与y轴相交于点C.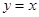 上的一个动点,点Q是抛物线上的一个动点,若以点O,C,P和Q为顶点的四边形为直角梯形,求相应的点P的坐标.
上的一个动点,点Q是抛物线上的一个动点,若以点O,C,P和Q为顶点的四边形为直角梯形,求相应的点P的坐标.