Question

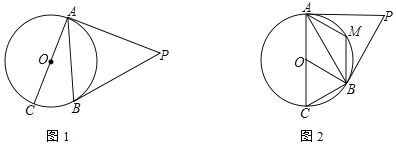
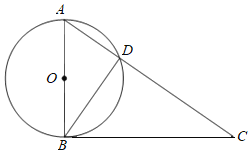
【题目】如图，AB是⊙O的直径，∠A＝∠CBD．

（1）求证：BC是⊙O的切线．

（2）若∠C＝35°，AB＝6，求的长（结果保留π）．

Answer 1

【答案】（1）证明见解析；（2）．

【解析】

（1）由圆周角定理得出∠ADB＝90°，得出∠A+∠ABD＝90°，证得∠ABC＝90°，即可得出BC是⊙O的切线.

（2）连接OD，可证得∠ABD＝∠C＝35°，由圆周角定理可得∠AOD＝2∠ABD＝70°，再通过弧长公式计算，即可得出答案.

（1）证明：∵AB是⊙O的直径，

∴∠ADB＝90°，

∴∠A+∠ABD＝90°，

∵∠A＝∠CBD，

∴∠CBD+∠ABD＝90°，即∠ABC＝90°，

∴BC⊥AB，

∴BC是⊙O的切线．

（2）解：连接OD，如图所示：

∵∠ABC＝90°，

∴∠C+∠A＝90°，

又∠A+∠ABD＝90°，

∴∠ABD＝∠C＝35°，

∴∠AOD＝2∠ABD＝70°，

∵直径AB＝6，

∴OA＝3，

∴的长＝＝．