题目内容
 如图,在直角梯形OABC中,AB∥OC,O为坐标原点,点A在y轴正半轴上,点C在x轴正半轴上,点B的坐标为(2,
如图,在直角梯形OABC中,AB∥OC,O为坐标原点,点A在y轴正半轴上,点C在x轴正半轴上,点B的坐标为(2, ),∠BCO=60,OH⊥BC,垂足为H.动点P从点H出发,沿线段HO向点O运动,动点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度.设点P运动的时间为t s.
),∠BCO=60,OH⊥BC,垂足为H.动点P从点H出发,沿线段HO向点O运动,动点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度.设点P运动的时间为t s.
(1)求OH的长;
(2)若△OPQ的面积为S(平方单位),求S与t之间的函数关系式.并求t为何值时,△OPQ的面积最大,最大值是多少?
解(1)∵AB∥OC,
∴∠OAB=∠AOC=90°,
在Rt△OAB中,AB=2,AO=2 ,
,
∴OB=4,∠ABO=60°,
∴BOC=60°,
而∠BCO=60°,
∴△BOC为等边三角形,
∴OH=2 ;
;
(2)∵OP=OH-PH=2 -t,
-t,
∴xp=3-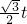 ,yp=
,yp= -
- ,
,
所以S= OQ×xp=
OQ×xp= ×t×(3-
×t×(3-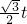 )=-
)=- t2+
t2+ (0<t<2
(0<t<2 ),
),
即S=-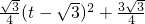
∴当t= 时,S最大=
时,S最大= .
.
分析:(1)判定△BOC为等边三角形后即可得到OH=AO=2 ;
;
(2)利用OP=OH-PH=2 -t,表示出点P的横纵坐标,然后利用三角形的面积公式计算三角形即可得到二次函数,配方后确定其最值即可;
-t,表示出点P的横纵坐标,然后利用三角形的面积公式计算三角形即可得到二次函数,配方后确定其最值即可;
点评:本题考查了二次函数的综合知识,特别是本题中涉及到的点的坐标与线段的长之间的互化,更是中考的热点考题之一.
∴∠OAB=∠AOC=90°,
在Rt△OAB中,AB=2,AO=2
 ,
,∴OB=4,∠ABO=60°,
∴BOC=60°,
而∠BCO=60°,
∴△BOC为等边三角形,
∴OH=2
 ;
;(2)∵OP=OH-PH=2
 -t,
-t,∴xp=3-
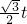 ,yp=
,yp= -
- ,
,所以S=
 OQ×xp=
OQ×xp= ×t×(3-
×t×(3-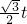 )=-
)=- t2+
t2+ (0<t<2
(0<t<2 ),
),即S=-
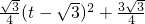
∴当t=
 时,S最大=
时,S最大= .
.分析:(1)判定△BOC为等边三角形后即可得到OH=AO=2
 ;
;(2)利用OP=OH-PH=2
 -t,表示出点P的横纵坐标,然后利用三角形的面积公式计算三角形即可得到二次函数,配方后确定其最值即可;
-t,表示出点P的横纵坐标,然后利用三角形的面积公式计算三角形即可得到二次函数,配方后确定其最值即可;点评:本题考查了二次函数的综合知识,特别是本题中涉及到的点的坐标与线段的长之间的互化,更是中考的热点考题之一.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
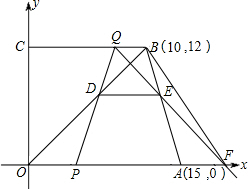 动时间为t(单位:秒).
动时间为t(单位:秒).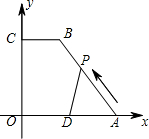 (10,0)、C(0,8),CB=4,D为OA中点,动点P自A点出发沿A→B→C→O的线路移动,速度为1个单位/秒,移动时间为t秒.
(10,0)、C(0,8),CB=4,D为OA中点,动点P自A点出发沿A→B→C→O的线路移动,速度为1个单位/秒,移动时间为t秒.
 单位,移动时间记为t秒.
单位,移动时间记为t秒. 如图,在直角梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,2),C(3,0).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ⊥直线OA,垂足为Q.设P点移动的时间为t秒(0<t≤7),△OPQ与直角梯形OABC重叠部分的面积为S.
如图,在直角梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,2),C(3,0).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ⊥直线OA,垂足为Q.设P点移动的时间为t秒(0<t≤7),△OPQ与直角梯形OABC重叠部分的面积为S.