题目内容
已知如图,△ABC中,AC=BC,BC与x轴平行,点A在x轴上,点C在y轴上,抛物线y=ax2-5ax+4经 过△ABC的三个顶点,
过△ABC的三个顶点,
(1)求出该抛物线的解析式;
(2)若直线y=kx+7将四边形ACBD面积平分,求此直线的解析式;
(3)若直线y=kx+b将四边形ACBD的周长和面积同时分成相等的两部分,请你确定y=kx+b中k的取值范围.(直接写出答案)
 解:(1)由题意可知,抛物线的对称轴为:
解:(1)由题意可知,抛物线的对称轴为: ,
,与y轴交点为c(0,4)
∴A(-3,0);B(5,4).
把A(-3,0)代入y=ax2-5ax+4得:9a+15a+4=0
解之得:
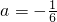
∴
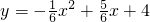 ;
;(2)直线y=kx+7将四边形ACBD面积平分,则直线一定经过OB的中点P.
根据题意可求P点坐标为(
 )
)把P(
 )代入y=kx+7得:k=-2,
)代入y=kx+7得:k=-2,∴直线的解析式为:y=-2x+7;
(3)
 .
.分析:(1)根据已知抛物线,利用对称轴公式代入数据即可得出对称轴,同时也可以得出C点的坐标,利用AC=BC,即可得出A点的坐标和B点的坐标,代入抛物线方程即可得出a的值,即得出该抛物线的解析式;
(2)结合题意,可知直线一定经过OB的中点P.又已知P点的坐标,代入直线方程,即可得出k的值,从而得出直线的方程;
(3)同(2);
点评:本题是二次函数的综合题型,其中涉及到的知识点有抛物线的顶点公式和三角形的面积求法.在求有关动点问题时要注意分析题意分情况讨论结果.

练习册系列答案
相关题目
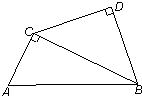 已知如图,△ABC中,∠ACB=90°,△BCD中,∠D=90°,CD=BD,又AC=6,tan∠ABC=
已知如图,△ABC中,∠ACB=90°,△BCD中,∠D=90°,CD=BD,又AC=6,tan∠ABC= 7、已知如图,△ABC中,D在BC上,且∠1=∠2,请你在空白处填一个适当的条件:当
7、已知如图,△ABC中,D在BC上,且∠1=∠2,请你在空白处填一个适当的条件:当 已知如图,△ABC中,BD⊥AC于D,tanA=
已知如图,△ABC中,BD⊥AC于D,tanA= 已知如图在△ABC中,∠ACB=90°,CD⊥AB于D,∠A的平分线交CD于F,BC于E,过点E作EH⊥AB于H.求证:EC=CF=EH.
已知如图在△ABC中,∠ACB=90°,CD⊥AB于D,∠A的平分线交CD于F,BC于E,过点E作EH⊥AB于H.求证:EC=CF=EH.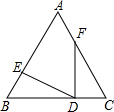 已知如图:△ABC中,AB=AC,BE=CD,BD=CF,则∠EDF=( )
已知如图:△ABC中,AB=AC,BE=CD,BD=CF,则∠EDF=( )