题目内容
已知：如图在矩形ABCD中，点E为CD的中点，连接EA、EB． 求证：∠EAB=∠EBA．
证明：∵点E为CD的中点，
∴DE=CE，
在△ADE和△BCE中，
，
△ADE≌△BCE．
∴AE=BE，
∴∠EAB=∠EBA．
分析：矩形的四个角都是直角，矩形的对边相等，以及等腰三角形中等边对等角．
点评：本题考查矩形的性质和等腰三角形的性质，熟记这些性质定理可求出解．
∴DE=CE，
在△ADE和△BCE中，
，△ADE≌△BCE．
∴AE=BE，
∴∠EAB=∠EBA．
分析：矩形的四个角都是直角，矩形的对边相等，以及等腰三角形中等边对等角．
点评：本题考查矩形的性质和等腰三角形的性质，熟记这些性质定理可求出解．
练习册系列答案
阅读快车系列答案
相关题目
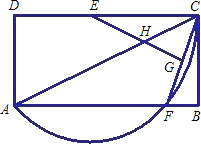EC为半径的圆上，连接CF，作EG⊥CF于G，交AC于H．已知AB=6，设BC=x，AF=y．
上，AH=2，连接CF．
（2010•北海）已知，如图在小正方形组成的网格中，矩形ABCD的顶点和点O都在格点上，将矩形ABCD绕点O顺时针方向旋转90°，得到矩形A'B'C'D'．
已知：如图，矩形AOBC的两边在坐标轴上，边长AO为2、OB为3，双曲线y=
已知：如图，矩形ABCD，M、N分别为AB、CD的中点，将A点折叠至MN上，落在A'点的位置，折痕为BE．