题目内容
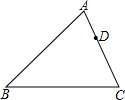
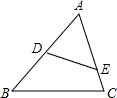
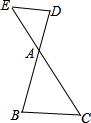
已知：如图，在△ABC中，AB=AC，D为CB延长线上一点，E为BC延长线上一点，且满足AB2=DB•CE．求证：△ADB∽△EAC．
证明：∵AB=AC∴∠ABC=∠ACB，
∴∠ABD=∠ACE，
∵AB2=DB•CE
∴
=
∴
=
∴△ADB∽△EAC．
∴∠ABD=∠ACE，
∵AB2=DB•CE
∴
| AB |
| CE |
| DB |
| AB |
∴
| AB |
| CE |
| DB |
| AC |
∴△ADB∽△EAC．
练习册系列答案
阅读快车系列答案
相关题目
