题目内容
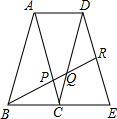
如图,矩形ABCD中,E为DC的中点,AD: AB= 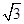 :2,CP:BP=1:2,连接EP并延长,交AB的延长线于点F,AP、BE相交于点O.下列结论:①EP平分∠CEB;②△EBP∽△EFB;③△ABP∽△ECP;④AO
:2,CP:BP=1:2,连接EP并延长,交AB的延长线于点F,AP、BE相交于点O.下列结论:①EP平分∠CEB;②△EBP∽△EFB;③△ABP∽△ECP;④AO AP=OB2.其中正确的序号是_______________.(把你认为正确的序号都填上)
AP=OB2.其中正确的序号是_______________.(把你认为正确的序号都填上)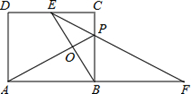
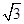 :2,CP:BP=1:2,连接EP并延长,交AB的延长线于点F,AP、BE相交于点O.下列结论:①EP平分∠CEB;②△EBP∽△EFB;③△ABP∽△ECP;④AO
:2,CP:BP=1:2,连接EP并延长,交AB的延长线于点F,AP、BE相交于点O.下列结论:①EP平分∠CEB;②△EBP∽△EFB;③△ABP∽△ECP;④AO AP=OB2.其中正确的序号是_______________.(把你认为正确的序号都填上)
AP=OB2.其中正确的序号是_______________.(把你认为正确的序号都填上)
①②③
试题分析:由条件设AD=
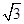 x,AB=2x,就可以表示出CP=
x,AB=2x,就可以表示出CP= x,BP=
x,BP= x,用三角函数值可以求出∠EBC的度数和∠CEP的度数,就可以求出∠CEP=∠BEP,运用勾股定理及三角函数值就可以求出就可以求出BF、EF的值,从而可以求出结论.
x,用三角函数值可以求出∠EBC的度数和∠CEP的度数,就可以求出∠CEP=∠BEP,运用勾股定理及三角函数值就可以求出就可以求出BF、EF的值,从而可以求出结论.设AD=
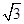 x,AB=2x,
x,AB=2x,∵四边形ABCD是矩形,
∴AD=BC,CD=AB,∠D=∠C=∠ABC=90°.DC∥AB,
∴BC=
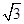 x,CD=2x,
x,CD=2x,∵CP:BP=1:2,
∴CP=
 x,BP=
x,BP= x
x∵E为DC的中点,
∴CE=
 CD=x,
CD=x,
∴∠CEP=30°,∠EBC=30°,
∴∠CEB=60°,
∴∠PEB=30°,
∴∠CEP=∠PEB,
∴EP平分∠CEB,故①正确;
∵DC∥AB,
∴∠CEP=∠F=30°,
∴∠F=∠EBP=30°,∠F=BEF=30°,
∴△EBP∽△EFB,

∴BE.BF=BP.EF.
∵∠F=BEF,
∴BE=BF,
∴BF2=PB•EF
∴△ABP∽△ECP
则正确的序号是①②③.
点评:本题综合性强,难度较大,是中考常见题,学生需熟练掌握平面图形的基本性质.

练习册系列答案
相关题目
 ,这两地的实际距离是
,这两地的实际距离是  .
.


 ,则
,则 .
. ,AB=AC=2
,AB=AC=2