Question

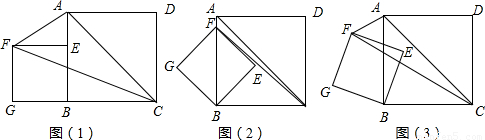
如图（1），点E是正方形ABCD边AB上的一动点（不与A、B重合），四边形EFGB也是正方形．正方形BEFG、ABCD的边长分别为a、b，且（a＜b），设△AFC的面积为S．
（1）请证明S为定值；
（2）将图（1）中正方形BEFG绕点B顺时针转动45°，如图（2），求S值；
（3）当点E处在AB中点（即b=2a时），将正方形BEFG绕点B旋转任意角度，如图（3），请直接写出旋转过程中S的最大值为：______．

Answer 1

【答案】分析：（1）连接FB，根据已知可得到△ABC与△AFC是同底等高的三角形，由已知可求得△ABC的面积为大正方形面积的一半，从而不难求得S的值．
（2）根据图形的关系，可得BF的长，根据三角形面积公式，可得△AFC的面积；
（3）分析可得：当F点到AC的距离取得最大、最小值时，S_△AFC取得最大、最小值．
解答：（1）证明：如图（1），连接FB．
∵四边形EFGB和四边形ABCD都是正方形，
∴∠FBA=∠BAC=45°，∴FB∥AC，
∴△AFC与△ABC是同底等高的三角形．
∴S_△AFC=S_△ABC
∵2S_△ABC=S_□ABCD，S_□ABCD=b²，
∴S=b²．即S为定值；

（2）∵点F在AB上，
∴BF²=a²+a²，即BF=a，
∴AF=b-a，
∴S_△AFC=AF•BC=（b-a）b=b²-ab；

（3）正方形EFGB在绕B点旋转的过程中，F点的轨迹是以点B为圆心，BF为半径的圆．
当b=2a时，存在最大值，不存在最小值．
∴S_△AFC的最大值=×b×（b+a）=a×2a=4a²（或b²）．
故填：4a²（或b²）．
点评：本题考查了旋转的性质、勾股定理及正方形的性质，解答本题要充分利用正方形的特殊性质，注意在正方形中的特殊三角形的应用，搞清楚矩形、菱形、正方形中的三角形的三边关系，可有助于提高解题速度和准确率．