题目内容
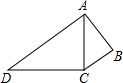
将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合.已知AB=2
,E是AC上的一点(AE>CE),且DE=BE,则AE的长为______.

| 3 |

∵AB=2
,∠BAC=30°,
∴BC=
AB=
×2
=
,
根据勾股定理,AC=
=
=3,
过点D作DF⊥AC于F,
∵△ACD是等腰直角三角形,
∴DF=CF=
AC=
,
设CE=x,则EF=
-x,
在Rt△DEF中,DE2=DF2+EF2=(
)2+(
-x)2,
在Rt△BCE中,BE2=BC2+CE2=
2+x2,
∵DE=BE,
∴(
)2+(
-x)2=
2+x2,
解得x=
,
所以,AE=AC-CE=3-
=
.
故答案为:
.

| 3 |
∴BC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
根据勾股定理,AC=
| AB2-BC2 |
(2
|
过点D作DF⊥AC于F,
∵△ACD是等腰直角三角形,
∴DF=CF=
| 1 |
| 2 |
| 3 |
| 2 |
设CE=x,则EF=
| 3 |
| 2 |
在Rt△DEF中,DE2=DF2+EF2=(
| 3 |
| 2 |
| 3 |
| 2 |
在Rt△BCE中,BE2=BC2+CE2=
| 3 |
∵DE=BE,
∴(
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
解得x=
| 1 |
| 2 |
所以,AE=AC-CE=3-
| 1 |
| 2 |
| 5 |
| 2 |
故答案为:
| 5 |
| 2 |


练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目