题目内容
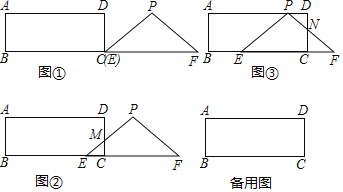
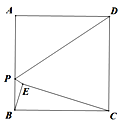
【题目】已知矩形![]() 中,
中,![]() 米,
米,![]() 米,
米,![]() 为
为![]() 中点,动点
中点,动点![]() 以2米/秒的速度从
以2米/秒的速度从![]() 出发,沿着
出发,沿着![]() 的边,按照A
的边,按照A![]() E
E![]() D
D![]() A顺序环行一周,设
A顺序环行一周,设![]() 从
从![]() 出发经过
出发经过![]() 秒后,
秒后,![]() 的面积为
的面积为![]() (平方米),求
(平方米),求![]() 与
与![]() 间的函数关系式.
间的函数关系式.
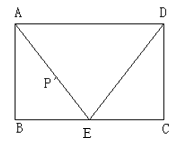
【答案】当点P在线段AE上时,y=![]() ;点P在线段ED上时,y=
;点P在线段ED上时,y=![]() ;点P在线段AD上时, y=32-4x.
;点P在线段AD上时, y=32-4x.
【解析】
分别求出当点P在线段AE上时,点P在线段ED上时,点P在线段AD上时,△ABP的边AB上的高,根据三角形的面积公式可得![]() 与
与![]() 间的函数关系式;
间的函数关系式;
解:∵![]() ,
,![]() 是
是![]() 中点
中点
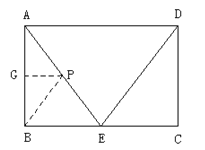
∴![]()
当![]() ,即
,即![]() 在
在![]() 上时,
上时,
过![]() 作
作![]() ,则
,则![]()
∴△AGP∽△ABE
∴![]() ,∴
,∴![]() ,
,
∴![]()
∴![]() ;
;
当![]() ,即
,即![]() 在
在![]() 上时,AE+EP=2x,DP=10-2x,
上时,AE+EP=2x,DP=10-2x,
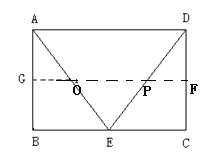
过![]() 作
作![]() 于G,交AE于O,交CD于F,则
于G,交AE于O,交CD于F,则![]() ,
,
∵四边形ABCD是矩形,
∴∠B=∠C=90°,AB=DC,AD=BC.
∵E为BC中点,
∴BE=EC.
∴△ABE≌△DCE.
∴AE=DE=5,
∵PG∥BE
∴△DPF∽△DEC
∴![]() ,即
,即![]()
∴PF=![]() ,
,
∴PG=6-(![]() )=
)=![]() ,
,
∴![]() ,即y=
,即y=![]() ;
;
当![]() ,即
,即![]() 在
在![]() 上时,AE+DE+DP=2x,AP=16-2x,
上时,AE+DE+DP=2x,AP=16-2x,
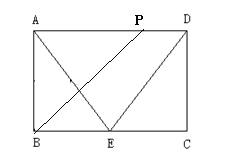
![]() ,
,
即y=32-4x.
故答案为:当点P在线段AE上时,y=![]() ;点P在线段ED上时,y=
;点P在线段ED上时,y=![]() ;点P在线段AD上时, y=32-4x.
;点P在线段AD上时, y=32-4x.

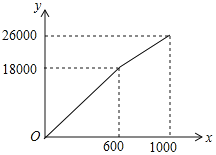
【题目】为了创建“全国文明城市”,鄂州市积极主动建设美丽家园,某社区拟将一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草面积为x(m2),种草费用y1(元)与x(m2)的函数关系式为y1=![]() ,其图象如图所示:栽花所需费用y2(元)与x(m2)的函数关系如表所示:
,其图象如图所示:栽花所需费用y2(元)与x(m2)的函数关系如表所示:
x(m2) | 100 | 200 | 300 |
y2(元) | 3900 | 7600 | 11100 |
(1)请直接写出y1与种草面积x(m2)的函数关系式,y2与栽花面积x(m2)的函数关系式;
(2)设这块1000m2空地的绿化总费用为W(元),请利用W与种草面积x(m2)的函数关系式,求出绿化总费用W的最大值;
(3)若种草部分的面积不少于600m2,栽花部分的面积不少于200m2,请求出绿化总费用W的最小值.