题目内容
【题目】已知△ABC三条边的长度分别是![]() ,
,![]() ,
,![]() ,记△ABC的周长为C△ABC.
,记△ABC的周长为C△ABC.
(1)当x=2时,△ABC的最长边的长度是 (请直接写出答案);
(2)请求出C△ABC(用含x的代数式表示,结果要求化简);
(3)我国南宋时期数学家秦九韶曾提出利用三角形的三边长求面积的秦九韶公式:S=![]() .其中三角形边长分别为a,b,c,三角形的面积为S.
.其中三角形边长分别为a,b,c,三角形的面积为S.
若x为整数,当C△ABC取得最大值时,请用秦九韶公式求出△ABC的面积.
【答案】(1)3;(2)![]() ;(3)
;(3)![]()
【解析】
(1)x=2代入三边表达式可得答案;
(2)由根式有意义可得![]() ,可得x的取值范围,
,可得x的取值范围,![]() ,
,![]() ,可得
,可得![]() 的值;
的值;
(3) 由(2)可得![]() ,且
,且![]() ,x为整数,将x的值可以从大到小依次验证,可得当当
,x为整数,将x的值可以从大到小依次验证,可得当当![]() 时,可得S的值.
时,可得S的值.
(1)3
(2)由根式有意义可得![]() ,即
,即![]() .
.
可得![]() ,
,![]() .
.
所以![]() =
=![]()
![]() .
.
(3)由(2)可得![]() ,且
,且![]() .
.
由于x为整数,且要使![]() 取得最大值,所以x的值可以从大到小依次验证.
取得最大值,所以x的值可以从大到小依次验证.
当![]() 时,三条边的长度分别是
时,三条边的长度分别是![]() ,
,
但此时![]() ,不满足三角形三边关系.
,不满足三角形三边关系.
所以![]() .
.
当![]() 时,三条边的长度分别是
时,三条边的长度分别是![]() ,满足三角形三边关系.
,满足三角形三边关系.
故此时![]() 取得最大值为7,符合题意.
取得最大值为7,符合题意.
不妨设a=2, b=2, c=3, 得
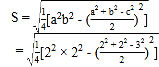
![]()
![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目