题目内容
| |||||||||||||||
答案:
解析:
解析:
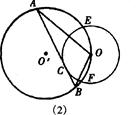
(1) |
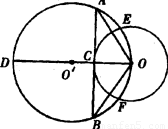
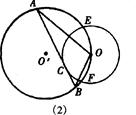
连结DB,则∠DBO=90° ∵AB切⊙O于点C∵.AB⊥OD,又OD是⊙O’直径,即OA=OB 得OA2=OC·OD=r·2R=2Rr.即OA·OB=2rR (也可证明△OBD∽△OCA) |
(2) |
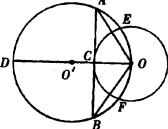
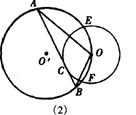
无变化 连结00',并延长交⊙O'于D点,连结DB、OC. 证明△OCA∽△OBD,得OA·OB=OC·OD=r·2R=2Rr |
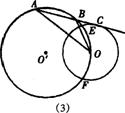
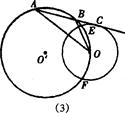
(3) |
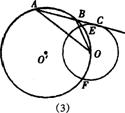
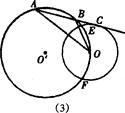
无变化 连结00’,并延长交⊙O’于B点,连结DB、OC 证出△OCA∽△OBD,得OA·OB=OC·OD.:r·2R=2Rr |

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案
相关题目




 经过半径为r的⊙O的圆心,⊙O与⊙
经过半径为r的⊙O的圆心,⊙O与⊙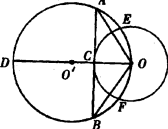
 经过半径为r的⊙O的圆心,⊙O与⊙
经过半径为r的⊙O的圆心,⊙O与⊙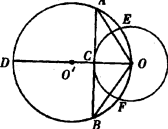
 经过半径为r的⊙O的圆心,⊙O与⊙
经过半径为r的⊙O的圆心,⊙O与⊙