题目内容
抛物线y=x2-2x-3的对称轴是直线 ．
【答案】分析：利用顶点坐标公式，可求顶点横坐标，即为对称轴．也可以利用配方法求对称轴．
解答：解：解法1：利用公式法
y=ax2+bx+c的顶点坐标公式为（
，
），代入数值求得对称轴是直线x=1；
解法2：利用配方法
y=x2-2x-3=x2-2x+1-4=（x-1）2-4，故对称轴是直线x=1．
故答案为：x=1．
点评：求抛物线的顶点坐标、对称轴及最值通常有两种方法：（1）公式法；（2）配方法．
解答：解：解法1：利用公式法
y=ax2+bx+c的顶点坐标公式为（
，），代入数值求得对称轴是直线x=1；解法2：利用配方法
y=x2-2x-3=x2-2x+1-4=（x-1）2-4，故对称轴是直线x=1．
故答案为：x=1．
点评：求抛物线的顶点坐标、对称轴及最值通常有两种方法：（1）公式法；（2）配方法．
练习册系列答案
阅读快车系列答案
相关题目
抛物线y=x2+2x-2的图象上最低点的坐标是（ ）
| A、（2，-2） | B、（1，-2） | C、（1，-3） | D、（-1，-3） |
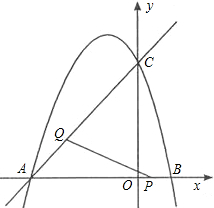秒，请求出△APQ的面积S与t的函数关系式，并求出当t为何值时，△APQ的面积最大，最大面积是多少？