题目内容
在△ABC中,∠B=38°,AD是BC边上的高,并且AD2=BD•DC,则∠BCA的度数为________.
52°或128°
分析:分两种情况考虑:当∠BCA为锐角和钝角,将已知的积的恒等式化为比例式,再根据夹角为直角相等,利用两边对应成比例且夹角相等的两三角形相似可得出△ADB∽△CDA,由相似三角形的对应角相等,利用直角三角形的两锐角互余及外角性质分别求出两种情况下∠BCA的度数即可.
解答: 解:分两种情况:
解:分两种情况:
①当∠BCA为锐角时,如图1所示,
∵AD2=BD•DC,
∴ =
=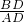 ,
,
又AD⊥BC,
∴∠ADB=∠CDA=90°,
∴△ADB∽△CDA,
∴∠B=∠CAD=38°,∠BAD=∠BCA.
在Rt△ADB中,∠ADB=90°,∠B=38°,
∴∠BAD=52°,
∴∠BCA=∠BAD=52°;
②当∠BCA为钝角时,如图2所示,
同理可得△ADB∽△CDA,又∠B=38°,
可得∠CAD=∠B=38°,
则∠BCA=∠CDA+∠CAD=128°.
综上,∠BCA的度数为52°或128°.
故答案为:52°或128°.
点评:此题考查了相似三角形的判定与性质,直角三角形的性质,以及外角的性质,利用了分类讨论的思想,其中相似三角形的判定方法有:两对对应角相等的两三角形相似;三边对应成比例的两三角形相似;两边对应成比例且夹角相等的两三角形相似.
分析:分两种情况考虑:当∠BCA为锐角和钝角,将已知的积的恒等式化为比例式,再根据夹角为直角相等,利用两边对应成比例且夹角相等的两三角形相似可得出△ADB∽△CDA,由相似三角形的对应角相等,利用直角三角形的两锐角互余及外角性质分别求出两种情况下∠BCA的度数即可.
解答:
 解:分两种情况:
解:分两种情况:①当∠BCA为锐角时,如图1所示,
∵AD2=BD•DC,
∴
 =
=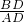 ,
,又AD⊥BC,
∴∠ADB=∠CDA=90°,
∴△ADB∽△CDA,
∴∠B=∠CAD=38°,∠BAD=∠BCA.
在Rt△ADB中,∠ADB=90°,∠B=38°,
∴∠BAD=52°,
∴∠BCA=∠BAD=52°;
②当∠BCA为钝角时,如图2所示,
同理可得△ADB∽△CDA,又∠B=38°,
可得∠CAD=∠B=38°,
则∠BCA=∠CDA+∠CAD=128°.
综上,∠BCA的度数为52°或128°.
故答案为:52°或128°.
点评:此题考查了相似三角形的判定与性质,直角三角形的性质,以及外角的性质,利用了分类讨论的思想,其中相似三角形的判定方法有:两对对应角相等的两三角形相似;三边对应成比例的两三角形相似;两边对应成比例且夹角相等的两三角形相似.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
在△ABC中,∠C=90°,BC=12,AB=13,则tanA的值是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中,a=
,b=
,c=2
,则最大边上的中线长为( )
| 2 |
| 6 |
| 2 |
A、
| ||
B、
| ||
| C、2 | ||
| D、以上都不对 |
 23、如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
23、如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
 18、如图,在△ABC中,边AC的垂直平分线交BC于点D,交AC于点E、已知△ABC中与△ABD的周长分别为18cm和12cm,则线段AE的长等于
18、如图,在△ABC中,边AC的垂直平分线交BC于点D,交AC于点E、已知△ABC中与△ABD的周长分别为18cm和12cm,则线段AE的长等于