Question

【题目】如图1，已知线段AB的两个端点坐标分别为A（a，1），B（﹣2，b），且满足 + =0．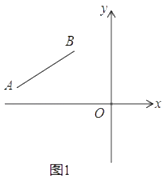

（1）则a= ， b=；
（2）在y轴上是否存在点C，使三角形ABC的面积等于8？若存在，请求出点C的坐标；若不存在，请说明理由；
（3）如图2，将线段BA平移得到线段OD，其中B点对应O点，A点对应D点，点P（m，n）是线段OD上任意一点，求证：3n﹣2m=0．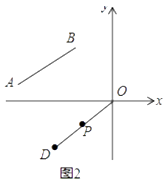

Answer 1

【答案】
（1）-5；3
（2）

存在，理由：如图1，

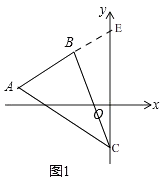
延长AB交y轴于E，

设C（0，c），

∵a=﹣5，b=3，

∴A（﹣5，1），B（﹣2，3），

∴AB的解析式为y= x+ （﹣5≤x≤﹣2），

∴E（0， ），

∴CE=|c﹣ |，

∵S△ABC=8，

∴S△ABC=S△ACE﹣S△BCE= CE|xA|﹣ CE|xB|= CE（|xA|﹣|xB|）= ×|c﹣ |×（5﹣2）=8，

∴c= 或c=﹣ ，

∴C（0， ）或（0，﹣ ）

（3）

∵将线段BA平移得到线段OD，

∴OD的解析式为y= x（﹣3≤x≤0），

∵点P（m，n）在线段OD上，

∴n= m，

∴3n﹣2n=0．

【解析】解：（1）∵ + =0．
∴a+5=0，b﹣3=0，
∴a=﹣5，b=3，
故答案：﹣5，3；
【考点精析】关于本题考查的确定一次函数的表达式和三角形的面积，需要了解确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法；三角形的面积=1/2×底×高才能得出正确答案．