题目内容
4. 如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.
如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.(1)求b、c的值;
(2)若只沿y轴上下平移该抛物线后与y轴的交点为A1,顶点为M1,且四边形AMM1A1是菱形,写出平移后抛物线的表达式.
分析 (1)已知了抛物线图象上A、B两点的坐标,将它们代入抛物线的解析式中,即可求得m、n的值.
(2)把解析式化成顶点式,求得顶点M的坐标,根据A、M的坐标,易求得AM的长;根据平移的性质知:若四边形A A′B′B为菱形,那么必须满足AA1=AM,由此可确定平移的距离,根据“上加下减”的平移规律即可求得平移后的抛物线解析式.
解答 解:(1)抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,则有:$\left\{\begin{array}{l}{c=3}\\{1+b+c=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=-4}\\{c=3}\end{array}\right.$;
故b=--4,c=3.
(2)由(1)得:y=x2-4x+3=(x-2)2-1;
∴M(2,-1),
∵A(0,3),
∴AM=$\sqrt{{2}^{2}+(-1-3)^{2}}$=2$\sqrt{5}$,
由平移可知:AA1∥MM1,AA1=MM1,
当AA1=AM=2$\sqrt{5}$时,四边形AMM1A1是菱形,
故抛物线需向下平移2$\sqrt{5}$个单位,即:
y=x2-4x+3+2$\sqrt{5}$或y=x2-4x+3-2$\sqrt{5}$.
点评 此题考查了二次函数解析式的确定、函数图象的平移、菱形的判定和性质,注意(2)有上移和下移两种情况.

练习册系列答案
相关题目
19.已知一元二次方程x2-4x+m=0有一个根为-2,则这个方程的另一个根为( )
| A. | 3 | B. | 4 | C. | 6 | D. | -6 |
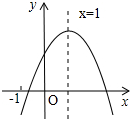 二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②a+c>b;③4a+2b+c>0;④2c<3b;⑤m(am+b)<a+b,(m≠1的实数)其中正确的结论有3个.
二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②a+c>b;③4a+2b+c>0;④2c<3b;⑤m(am+b)<a+b,(m≠1的实数)其中正确的结论有3个.