题目内容
如图,已知点D为等腰直角△ABC内一点,∠ACB=90°,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.

(1)求证:DE平分∠BDC;
(2)若点M在DE上,且DC=DM,求证: ME=BD.
【答案】
证明见解析
【解析】(1)在等腰直角△ABC中,
∵AC=BC
∵∠CAD=∠CBD=15o,
∴∠BAD=∠ABD=45o-15o=30o,
∴BD=AD,
在△BDC和△ACD中

∴△BDC≌△ADC,
∴∠DCA=∠DCB=45o.
由∠BDM=∠ABD+∠BAD=30o+30o=60o,
∠EDC=∠DAC+∠DCA=15o+45o=60o,
∴∠BDM=∠EDC,
∴DE平分∠BDC;
(2)如图,连接MC,
∵DC=DM,且∠MDC=60°,
∴△MDC是等边三角形,即CM=CD.
又∵∠EMC=180°-∠DMC=180°-60°=120°,
∠ADC=180°-∠MDC=180°-60°=120°,
∴∠EMC=∠ADC.
又∵CE=CA,
∴∠DAC=∠CEM=15°,
∴△ADC≌△EMC,∴ME=AD=DB.
(1)灵活运用等腰三角形的性质,全等三角形的判定及全等三角形的性质,计算∠BDM和∠EDC的度数即可
(2)综合运用等边三角形的判定和它的性质,找全等三角形的条件即可
|

练习册系列答案
相关题目
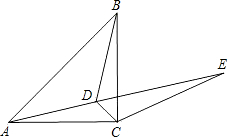 如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°.
如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°.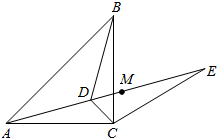 如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.
如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.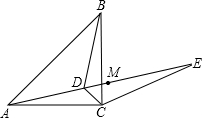 (2012•梁子湖区模拟)如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.若点M在DE上,且DC=DM,试探究线段ME与BD的数量关系,并说明理由.
(2012•梁子湖区模拟)如图,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.若点M在DE上,且DC=DM,试探究线段ME与BD的数量关系,并说明理由. 如图,已知点D为等腰直角△ABC内一点,AC=BC,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.若DE=acm,BD=bcm(a>b),则CD=
如图,已知点D为等腰直角△ABC内一点,AC=BC,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.若DE=acm,BD=bcm(a>b),则CD=