题目内容
解下列方程:
(1) =1;
=1;
(2) .
.
解:(1) =1,
=1,
方程两边同乘以(1-x)(3-x),
得2(3-x)-x(1-x)+(2x-1)=(1-x)(3-x),
去括号,得6-2x-x+x2+2x-1=3-3x-x+x2,
整理,得3x=-2,
解得:x=- .
.
检验:当x=- 时,(1-x)(3-x)≠0,
时,(1-x)(3-x)≠0,
∴x=- 是原方程的解.
是原方程的解.
(2) ,
,
原方程可化为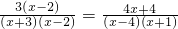 ,
,
约分,得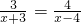 ,
,
方程两边同乘以(x+3)(x-4),
得:3(x-4)=4(x+3),
3x-12=4x+12,
-x=24,
∴x=-24,
检验:当x=-24时,(x+3)(x-4)≠0,
∴x=-24是原方程的解.
分析:(1)的最简公分母是(1-x)(3-x),
(2)约分后最简公分母是(x+3)(x-4),然后去分母化为整式方程求解.
点评:(1)解分式方程的基本思想是“转化思想”,方程两边都乘最简公分母,把分式方程转化为整式方程求解.
(2)解分式方程一定注意要代入最简公分母验根.
(3)能约分的分式方程应先约分进行化简.
 =1,
=1,方程两边同乘以(1-x)(3-x),
得2(3-x)-x(1-x)+(2x-1)=(1-x)(3-x),
去括号,得6-2x-x+x2+2x-1=3-3x-x+x2,
整理,得3x=-2,
解得:x=-
 .
.检验:当x=-
 时,(1-x)(3-x)≠0,
时,(1-x)(3-x)≠0,∴x=-
 是原方程的解.
是原方程的解.(2)
 ,
,原方程可化为
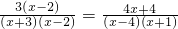 ,
,约分,得
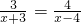 ,
,方程两边同乘以(x+3)(x-4),
得:3(x-4)=4(x+3),
3x-12=4x+12,
-x=24,
∴x=-24,
检验:当x=-24时,(x+3)(x-4)≠0,
∴x=-24是原方程的解.
分析:(1)的最简公分母是(1-x)(3-x),
(2)约分后最简公分母是(x+3)(x-4),然后去分母化为整式方程求解.
点评:(1)解分式方程的基本思想是“转化思想”,方程两边都乘最简公分母,把分式方程转化为整式方程求解.
(2)解分式方程一定注意要代入最简公分母验根.
(3)能约分的分式方程应先约分进行化简.

练习册系列答案
相关题目