题目内容
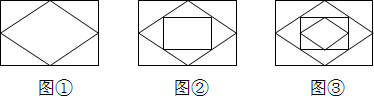
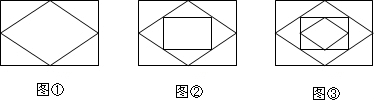
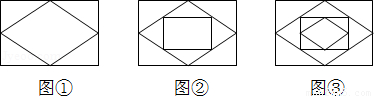
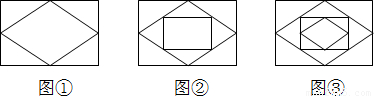
已知:顺次连接矩形各边的中点,得到一个菱形,如图①;再顺次连接菱形各边的中点,得到一个新的矩形,如图②;然后顺次连接新的矩形各边的中点,得到一个新的菱形,如图③;如此反复操作下去,则第2012个图形中直角三角形的个数有

- A.8048个
- B.4024个
- C.2012个
- D.1066个
B
:第1个图形,有4个直角三角形,
第2个图形,有4个直角三角形,
第3个图形,有8个直角三角形,
第4个图形,有8个直角三角形,
…,
依次类推,当n为奇数时,三角形的个数是2(n+1),当n为偶数时,三角形的个数是2n个,
所以,第2012个图形中直角三角形的个数是2×2012=4024.
故选B.
:第1个图形,有4个直角三角形,
第2个图形,有4个直角三角形,
第3个图形,有8个直角三角形,
第4个图形,有8个直角三角形,
…,
依次类推,当n为奇数时,三角形的个数是2(n+1),当n为偶数时,三角形的个数是2n个,
所以,第2012个图形中直角三角形的个数是2×2012=4024.
故选B.

练习册系列答案
相关题目