题目内容
【题目】如图(1)在Rt△ABC中,∠C=90°,AB=5cm.BC=a cm,AC=3cm,且a是方程x2﹣(m﹣1)x+m+4=0的根.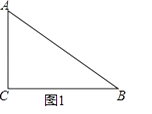
(1)求a和m的值;
(2)如图(2),有一个边长为 ![]() 的等边三角形DEF从C出发,以1cm/s的速度沿CB方向移动,至△DEF全部进入与△ABC为止,设移动时间为xs,△DEF与△ABC重叠部分面积为y,试求出y与x的函数关系式并注明x的取值范围;
的等边三角形DEF从C出发,以1cm/s的速度沿CB方向移动,至△DEF全部进入与△ABC为止,设移动时间为xs,△DEF与△ABC重叠部分面积为y,试求出y与x的函数关系式并注明x的取值范围;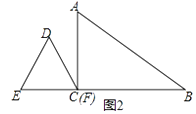
(3)试求出发后多久,点D在线段AB上?
【答案】
(1)
解:在Rt△ABC中,∠C=90°,AB=5cm.BC=a cm,AC=3cm,
根据勾股定理可得,BC=4cm,即a=4.
∵a是方程x2﹣(m﹣1)x+m+4=0的根
∴42﹣(m﹣1)×4+m+4=0的根,
∴m=8,
(2)
解:由(1)得a=4,则等边三角形DEF的边长为 ![]() =2(cm),
=2(cm),
如图(1),

当0≤x≤1时,易知∠DFC=60°,
∵∠ACF=90°,
∴∠CGF=30°,
∴CG= ![]() CF=
CF= ![]() x
x
∴y=S△CGF= ![]() CFCG=
CFCG= ![]() x
x ![]() x=
x= ![]() x2,
x2,
如图(2),
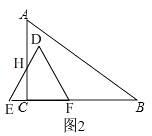
当1<x≤2时,BE=2﹣x,HC= ![]() EC=
EC= ![]() (2﹣x),
(2﹣x),
∴S△HEC= ![]() ECHC=
ECHC= ![]() (2﹣x)
(2﹣x) ![]() (2﹣x)=
(2﹣x)= ![]() (2﹣x)2,
(2﹣x)2,
∴y=S△DEF﹣S△HEC= ![]() ×22﹣
×22﹣ ![]() (2﹣x)2=﹣
(2﹣x)2=﹣ ![]() x2+2
x2+2 ![]() x﹣
x﹣ ![]()
综上, 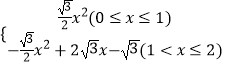
(3)
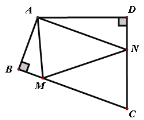
解:如图(3),

若点D在线段AB上,
过点D作DM⊥BC于点M,此时DM∥AC,
∴△BDM∽△BAC
∴ ![]() 即
即 ![]() ,
,
∴DM= ![]()
又等边三角形DEF的边长2,
∴DM= ![]()
∴ ![]() ,
,
∴x= ![]()
即出发后 ![]() s时,点D在线段AB上.
s时,点D在线段AB上.
【解析】(1)先利用勾股定理求出a,再用一元二次方程的解求出m;(2)分两种情况①利用三角形的面积公式,②利用三角形的面积差即可得出结论;(3)先判断出△BDM∽△BAC再用DM建立方程求解即可.
【考点精析】通过灵活运用三角形的面积和相似三角形的性质,掌握三角形的面积=1/2×底×高;对应角相等,对应边成比例的两个三角形叫做相似三角形即可以解答此题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案